10: def

In dieser Lektion zeigen wir dir die wichtigste Idee beim Programmieren: definiere deine eigenen Funktionen! Funktionen erlauben es dir, deine Programme kürzer zu machen, besser zu organisieren, leichter zu lesen und zu debuggen und besser wiederzuverwenden. In späteren Lektionen werden wir andere Vorteile sehen wie zum Beispiel Rekursion.

Eine Funktion definieren

Wir beginnen mit einem Beispiel. Erinnerst du dich an die Funktion abs? Sie nimmt ein Argument, nämlich eine Zahl x, und gibt deren "Absolutbetrag" zurück (der x ist, wenn x > 0 ist und -x wenn x < 0 ist).

Die Art und Weise, diese Funktion in Python zu definieren, sieht so aus:

def abs(x):     # definiere eine Funktion 'abs' mit einem Argument 'x'
  if x >= 0:    # Funktionskörper beginnt hier
    return x
  else:
    return -x   # Funktionskörper endet hier
(Klicke hier um diesen Code in der Konsole zu testen.)

Die zwei Teile einer Funktionsdefinition

Die erste Zeile in einer Funktionsdefinition spezifiziert den Namen der Funktion und die Argumente der Funktion. Sie sieht folgendermaßen aus:

def «function-name»(«argument-list»):

In dem obigen Beispiel ist abs der Name der Funktion und die Argumentliste enthält ein Argument x. Sie wird Argumentliste genannt, weil es mehrere Argumente geben kann, wie zum Beispiel x, y, z; es ist außerdem möglich, null Argumente zu haben, also eine leere Argumentliste. Die Argumente sind der Input der Funktion.

Alles nach der ersten Zeile einer Funktionsdefinition ist der Körper der Funktion. Der Körper ist ein eingerückter Codeblock. Wann immer die Funktion aufgerufen wird, wird der Körper ausgeführt mit Bezug auf diese Argumente/Inputs. Und schließlich, wenn wir diese Zeile im Körper der Funktion erreichen,

return «value»

hört die Funktion auf und gibt «value» als output aus. Das bedeutet, dass der ausgegebene Wert der Output der Funktion ist. Wie das abs Beispiel zeigt, kann der Körper mehrere return Statements beinhalten; aber nur das erste ausgeführte hat einen Effekt, da die Funktion danach aufhört, auszuführen.

Beispiel: Definition und Aufrufen einer Funktion

Das folgende Programm enthält eine Funktionsdefinition und einige andere Statements, die ausgeführt werden, nachdem die Funktion definiert wird.

Beispiel
Squaring function
Wir sehen, dass der Name der Funktion square ist, es gibt nur ein Argument x, und dass der Körper der Funktion nur aus einer Ausgabezeile x*x besteht. Weiterhin, außerhalb der Funktion, haben wir zwei Befehle, die die Funktion insgesamt dreimal aufrufen.

  1. Wenn der erste Befehl ausgeführt wird, muss Python square(10) evaluieren.
    • Python vergleicht die Liste von Inputs (10) mit der Argumentliste (x). Also führt es den Körper der Funktion return x*x aus, während es sich erinnert, dass x gleich 10 ist. So ergibt x*x das Ergebnis 100, das auch ausgegeben wird.
  2. Wenn der zweite Befehl ausgeführt wird, muss Python square(square(2)) ermitteln.
    • Der innere Teil square(2) wird zuerst bestimmt. Wir setzen zwischenzeitlich x gleich 2 und führen den Funktionskörper aus, der 4 ausgibt.
    • Dann wird der äußere Ausdruck evaluiert; da square(2) nämlich 4 ergibt, rufen wir nun square(4) auf. Dies ergibt 16, was ausgegeben wird.

Wie üblich, kannst du versuchen, herauszufinden, wie dies im Python3 Visualizer aussieht.

Vier häufige Fehler

Ein häufiger Fehler, den du beim Definieren einer Funktion machen kannst, ist es, das return Statement zu vergessen.

Beispiel
Fehler 1: return vergessen

Wie du sehen kannst, wenn kein return Statement im Körper angetroffen wird, ergibt die Funktion automatisch None. Also, wenn du bei einer Übung erfolglos bleibst, weil eine Funktion None ausgibt, ist das Problem oft, dass irgendein Funktionsinput nicht dazu führt, dass ein return Statement ausgeführt wird.

Es kann sein, dass du bewusst ein return Statement weglässt. Dies macht nur dann Sinn, wenn deine Funktion einen Nebeneffekt hat, der sich von seinem Ausgabewert unterscheidet, zum Beispiel die Ausgabe eines Outputs:
Beispiel: Ein Nebeneffekt und kein return Statement

Ein anderer häufiger Fehler ist es, zu vergessen, den Code einzurücken, was einen IndentationError zum Ergebnis hat.

Beispiel
Fehler 2: Vergessen, den Code einzurücken

Wie wir in Lektion 2 gesehen haben, führt das Aufrufen von zu wenigen oder zu vielen Argumenten zu einem Fehler.

Beispiel
Fehler 3: Zu viele Argumente aufgerufen

Schlussendlich, wenn du einen Tippfehler machst, wenn du die Funktion definierst oder sie aufrufst, wirst du einen Fehler erhalten, der dir sagt, dass die Funktion undefiniert ist.

Beispiel
Fehler 4: Falscher Name

Probiere es selbst aus

Für diese und zukünftige Übungen braucht kein input() oder print() verwendet zu werden, wenn du aufgefordert wirst, "eine Funktion zu programmieren". Wir werden für Dich die Funktion mit bestimmten Argumenten automatisch aufrufen und die Ergebnisse direkt bewerten, die die Funktion zurückgibt.

Eine richtige Lösung für diese Übung wird aus zwei Zeilen bestehen (siehe "Die zwei Teile einer Funktionsdefinition" am Anfang dieser Lektion).

Programmierübung: Cubism
Schreibe eine Funktion cube(n), die eine Zahl n als Eingabe nimmt und n * n * n zurückgibt.
Gib Testbefehle wie print(meinefunktion("Test-Argument")) unten ein.

Zwei oder mehr Argumente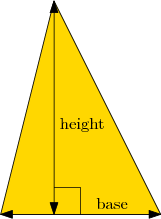

Die Funktionen oben nahmen nur ein Argument, aber eine Funktion kann so konstruiert sein, dass sie jedwede Zahl an Argumenten akzeptiert. Zum Beispiel hast du bereits input() mit 0 Argumenten verwendet (und in Lektion 15A wirst du selbst eine Funktion mit null Argumenten definieren).

Hier ist ein Beispiel mit zwei Argumenten aus der Geometrie. Stellen wir uns vor, wir brauchen eine Funktion, um die Fläche (engl.: area) eines Dreiecks zu berechnen, mit gegebener Länge der Grundlinie (engl.: base) und seiner Höhe (engl.: height).
Die Formel für die Fläche ist

area = base × height / 2

Dann können wir in Python eine Funktion triangleArea folgendermaßen definieren:

Beispiel
Eine Funkion mit zwei Argumenten

Eine andere wichtige zu beachtende Sache ist, dass es einen Unterschied macht,
wann eine Funktion definiert wird und wann sie ausgeführt wird.
Der Körper läuft nicht bis die Funktion tatsächlich aufgerufen wird.
Mach die folgende Übung um dies zu testen:

Multiple-Choice-Übung: In-n-Out
Was ist die Ausgabe des folgenden Programms?

def f():          # function of 0 arguments
   print("in f")
print("not in f")
f()               # call f now
Richtig! Die Funktion f wird vor allem als erstes definiert, aber ihr Körper nicht sofort ausgeführt. Nachdem die Funktion definiert ist, geben wir not in f aus. Dann wird die Funktion aufgerufen und ihr Körper ausgeführt, der in f ausgibt.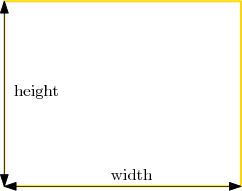

Wie du sehen kannst, ist die einzige Änderung die, dass wir def «function-name»(«argument1») ersetzt haben durch def «function-name»(«argument1», «argument2»).

In der letzten Übung bitten wir dich, deine eigene Funktion mit zwei Argumenten zu schreiben, um den Umfang eines Rechtecks zu berechnen (der Umfang ist die Gesamtlänge aller Seiten). In einem Rechteck mit vorgegebener Breite (engl.: width) und Höhe (engl.: height), wird sein Umfang von der folgenden Formel berechnet:

perimeter = width + height + width + height

Programmierübung: Rectangle
Schreibe eine Funktion rectanglePerimeter(width, height), die den Umfang eines Rechtecks bestimmt.
Gib Testbefehle wie print(meinefunktion("Test-Argument")) unten ein.

Rekursive Funktionsaufrufe

Funktionen sind die Basiskomponenten von gut konstruierten großen Programmen: du kannst die selbe Aufgabe zweimal machen, ohne den selben Code zweimal zu schreiben, und du kannst Lösungen für häufige Aufgaben wiederverwenden. Hier ist ein Beispiel dafür, eine Funktion zu schreiben und sie in einer anderen zu verwenden.

Beispiel
Kannst du erraten, was dieses Programm macht, bevor du es ausführst?
Erinnere dich an Lektion 4 daran, dass eine Multiplikation von Strings und ganzen Zahlen bedeutet, den String um diese Zahl zu wiederholen. So ist zum Beispiel "tar"*2 gleich "tartar".

Du bist jetzt bereit für die nächste Lektion!