[Interactive Python Textbook]

S3-2 Documenter vos fonctions

Posted on November 2, 2021 by jlt

I Les signatures dans la définition

La plupart des langages de programmation nécessitent la spécification du typage des variables,

En Python, ce n'est pas obligatoire, mais fortement recommandé.

Voici la syntaxe qu'il faut utiliser :

def nomFonction(argument: type) -> typeRetour:
		blocs des instructions
		return résultat

Exemple 1 : La fonction carré

Prend en paramètre un float
renvoie un float

Exemple 2 : La fonction est_pair

Prend en paramètre un int
renvoie un bool

II Nommage

Une fonction :

Renvoie un résultat
ou fait quelques chose

Dans le deux cas, c'est une ACTION, et on nomme (le plus souvent) un fonction par un verbe. Ceci est particulièrement important pour les fonction qui font quelques chose sans renvoyer de résultat.

La convention PEP8 donne l'habitude de nommer les fonctions (comme les variables) avec des lettres minuscules et des tirets bas (celui du "8") _.

Exemples : lire_fichier, resoudre_equation, creer_grille_vide etc...

Comme pour les noms de variables, il est absolument recommandé de ne pas utiliser de caractères accentués dans les noms des fonctions.

On préfère toutefois parfois (ou souvent suivant les personnes) la convention dite camelCase qui consiste a écrire en minuscules, mais si le nom est constitué de plusieurs mots, on met une majuscules à tous les mots sauf le premier. Exemples : lireFichier, resoudreEquation, creerGrilleVide etc...

Pour clarifier la fonction, il est conseillé d'utiliser un verbe dans son nom (obtenir, donner, get, set, ...).

III. La docstring

Il est important de documenter vos fonctions, c'est-à-dire de décrire en quelques phrases le rôle de la fonction, de donner des informations sur la fonction, le lien entre les entrées et la sortie.

Pour cela, juste en dessous de la première ligne définissant la fonction, il suffit de mettre ses informations :

"""
Entrées : <donner la nom des paramètres, leur rôle et leurs types>
Sortie : préciser ce que renvoie la fonction (en précisant le type) ou péciser qu'elle ne renvoie rien, et décrire e qu'elle fait
"""

C'est ce que l'on appelle (en bon franglais) la docstring de la fonction.

Exemple 1

Exemple 2

Exemple 3

L'intérêt de l'auto-documentation d'une fonction par un texte est double :

Pour vous : le faire vous oblige à réfléchir au contenu de votre fonction avant de la programmer ; c'est un gain d'efficacité,
Pour les utilisateurs de votre code (ou pour vous longtemps après avoir programmé la fonction) : Quand on saisit dans la console, après l'exécution de la fonction, l'instruction help(nom de la fonction), Python affiche le docstring de la fonction ce qui nous permet d'avoir des informations sur la fonction en cas d'oubli.

Exercices

Exercice 1

Exercice 2

S3-1 Les fonctions

Posted on November 2, 2021 by jlt

Définir une Fonction

La fonction valeur absolue

Nous allons commencer avec un exemple. Vous rappelez-vous de la fonction abs ? Elle prend seulement un argument (un nombre x), et retourne sa valeur absolue (qui devient x quand x ≥ 0 et -x quand x < 0). La façon de définir cette fonction dans Python est :

Nous pourrions coder la même fonction différemment, sans que cela ne fasse aucune différence dans la façon de l'utiliser.

Dans cette seconde version nous introduisons 2 fois l'instruction return. Ne perdez pas de vue que, dès lors qu'une instruction return est exécutée, la fonction s'arrête (et on reprend le programme appelant là ou on l'avait arrêté).

Notez que dans cette version nous n'initialisons pas la variable valeur absolue, c'est inutile, on n'utilise aucune variable, on renvoie simplement un résultat.

Exercices

Exercice 1 : Pythagore

Coding Exercise: Pythagore

Ci dessous, donne ici une fonction qui teste si a^2 +b^2 == c^2 et qui affiche si le triangle est rectangle. Cette fonction ne renvoie rien (None).

Modifiez cette procédure pour la transformer en une fonction qui renvoie True si l'égalité est vraie et False sinon.

Vous devez modifier :

Le corps de la fonction pour renvoyer True ou False
La docstring et la ligne de la définition de la fonction
les appels pour que le programme principal affiche le résultat de la fonction.

def est_rectangle(a,b,c) -> None:
    """
    Entrées : a b et c, trois nombres
    Sortie : Rien :
        si a^2 + b^2 = c^2,  la fonction AFFICHE : le triangle est rectangle
        sinon elle affiche : le triangle n'est pas rectangle
    """
    if a**2 + b**2 == c**2 :
        print("le triangle est rectangle")
    else :
        print("le triangle n'est pas rectangle")

est_rectangle(3, 4, 5)
est_rectangle(20, 21, 29)
est_rectangle(5, 5, 5)

Exercice 2 : multiple de 3

Coding Exercise: Multiples de 3

Ci dessous une donne une fonction qui affiche les multiple de 3 jusqu'à 100.

Modifiez la fonction mult3 pour qu'elle affiche les multiples de 3 jusqu'à un entier MAX qui sera passé en paramètre.

Vous devez :

Modifier la définition de la fonction, pour passer un paramètre suplémentaire n_max
modifier le corps de la fonction pour n\'afficher les multiples de 3 que jusqu'à n_max
modifier la docstring

Le correcteur va générer un entier n_max pour exécuter et tester la fonction.

def mult3() -> int:
    """
    Entrée : rien
    Sortie : rien (None)
    affiche les multiples de 3 inférieurs à 100
    """
    for i in range(3, 101):
        if i%3 == 0 :
            print(i)

Exercice 3 : puissance

Exercice 4 : plus grande valeur

Exercice 5 : Vitesse moyenne

T 3.5 j'apprend à penser récursif

Posted on October 13, 2021 by jlt

Dans les exercices que vous avez réalisés, vous avez souvent éprouvé des difficulté à trouver le cas de base, et le cas similaire plus simple.

En réalité, pour beaucoup, vous n'avez jamais réfléchi de cette façon !

Au lieu de cela, vous avez regardé les exercices précédents, et tenté de vous en inspirer. Cela vous amène à écrire des bouts de codes, qui, si vous avez bien respecté les Types renvoyés, sont plus ou moins correct, mais incomplet, non fonctionnel...

Respecter les types ?

qu'est-ce que j'entend par là ?

1er exemple : Reprenons l'exercice my_range(a,b)

L'énoncé donne les spécifications de la fonction, et on lit :

:returns : list: la liste des entiers de a à b - 1

Il faudra donc que votre cas de base ET votre cas général renvoient toujours une liste. Seule exception, on renvoie None si a > b.

donc si vous écrivez :

return a + my_range(a,b) vous additionnez un int (a) et une liste -> typeError
return [ my_range(a,b) ] Vous avez bien compris qu'il faut renvoyer une liste, mais my_range(a,b) est une liste donc ici vous renvoyez une liste contenant une liste, donc une liste de liste, pas une liste d'entiers

2ème exemple : Reprenons l'exercice longeur(chaine)

L'énoncé donne les spécifications de la fonction, et on lit :

:returns : int: le nombre de lettres dans la chaine

Il faudra donc que votre cas de base ET votre cas général renvoient toujours un entier.

donc si vous écrivez :

return txt[0] + longueur( txt[1:] ) vous additionnez un str (txt[0]) et un int car longueur(txt) est toujours un int -> typeError
if txt == "" : return "" vous retournez une chaine, pas un int

Dans ce dernier cas, on voit bien que vous avez senti la solution : traiter le premier caractère, puis le reste de la chaine. Bon, vous avez un peu du mal a écrire txt[1:] parce que les chaines de caractères vous ennuient un peu, mais souvent vous avez plus ou moins tenté d'écrire cela.

Il est donc important de bien faire attention au type que la fonction retourne et le cas général doit combiner des solution de même types. Une liste + une liste, un int + un int, un str plus un str etc....

penser récursif

C'est là que vous pêchez le plus. Imiter un exercice précédent ne fonctionne pas, ils sont tous un peu différent.

Reprenons les :

1er exemple : somme(a,b) doit renvoyer a+b (un int)
on ne peut ajouter/retrancher que 1, on ne sait donc pas additionner a et b.
quelle est le problème trivial ? on pourrait songer à : somme(a,1) qui consiste à ajouter 1 (on sait faire) ou bien à somme(a,0) qui consiste à ne rien ajouter, on sait faire.

alors quel est le cas qui se rapproche un peu de ce cas simple ? c'est quand b diminue et se rapproche de 1 ou de 0. d'ou l'idée de rappeler somme(a,b-1)

Cette étape de réflexion est indispensable, et doit vous mener à écrire :

a+b = a +1 + (b - 1)

il existe 2 façon de l'entendre :

somme(a,b) = 1 + somme(a,b-1)
somme(a,b) = somme(a+1,b-1)

les deux sont corrects. Exprimons cela avec une phrase en français :

pour ajouter b à a : j'ajoute 1 puis j'ajoute tout le reste (b-1)

2ème exemple : longueur de la chaine

La phrase en français serait :

c'est 1 + la longueur du reste de la chaine.

la relation de récurrence s'écrira donc :

longueur(txt) = 1 + longeur(txt sans la première lettre)

reste à savoir écrire en python l'expression txt sans la première lettre

3ème exemple : my_range

vous êtes d'accord que nous écrivons de gauche à droite ? donc il est assez peu logique de commencer par la droite....

prenez un exemple quand vous ne voyez pas de suite. Si vous devez écrire range(2,6) vous allez forcément écrire 2 puis 3 puis 4 puis etc... puis 5.

le etc ci-dessus vous indique la réponse ! il indique qu'on répète ce qu'on vient juste de faire jusqu'à la fin de la liste. Ce etc est en fait notre expression pour indiquer une récurrence.

La bonne formulation sera :

Je met 2 dans la liste puis je vais recommencer avec les autres, c'est à dire my_range(3,6)

Si on respecte les types, ce 2 doit être dans une liste : [2]

reste à généraliser, avec a et b au lieu de 2 et 6 :

la liste des entiers de 2 à 5 est [2] + liste des entiers de 3 à 5

En voulant vous inspirer d'un exercice précédent, beaucoup ont écrit quelques chose du genre :

my_range(a,b) = my_range(a,b-1)

pourquoi pas, mais aller de a à b-1 est pareil que aller de a à b-2 et ajouter b-1, vous écrivez de droite à gauche ? C'est un peu malheureux, ça complique inutilement l'exercice, d'autant que vous vous emmêlez dans les b-1....

C'est parce que vous n'avez pas pensé récursif, mais plutôt pensé "comment j'ai fait dans cet autre exercice ?"

3ème exemple : parité de l'entier n

pour cet exercice c'est le cas de base qui peut vous guider. Le problème indique qu'on a pas le droit d'utiliser modulo (%), mais ce qu'on cherche est bien de savoir si n%2 == 0

et c'est trivialement vrai si n = 0

donc on va devoir se rapprocher de ce cas trivial. connaitre la parité de n-1 est en ce sens un peu plus simple que connaitre la parité de n, car on se rapproche de 0.

quel lien existe-t-il entre parité de n, et parité de n-1 ? ben c'est l'opposé:

si n pair n-1 est impair

s n impair n-1 est pair

on peut donc écrire :

partité de n = not ( parité de n-1)

et nous avons notre récurence !

-> return not est_pair(n-1)

un dernier exemple : printInline(a,b)

Cette fonction est en réalité une procédure, elle ne renvoi rien (None). Elle doit au contraire afficher quelques chose.

On est dans une situation similaire quand on dessine, par exemple avec Turtle.

Pour respecter les types on ne pourra en aucun cas écrire quelques chose comme :

printInline(a,b) = quelques chose + printInline(a,b-1)

Car additionner quelques chose et None est impossible !

La fonction doit FAIRE une partie du travail. laquelle ?

Puisque nous devons écrire une liste d'entiers, commençons par le premier :

print(a)

puis continuons avec tous les autres en partant du prochain qui est a+1 : printInline(a+1,b)

restera à régler le problème du retour à la ligne : print(a) induit un retour à la ligne qu'il faudra remplacer par un espace sans retour à la ligne : print(a,end=" ").

reste aussi a trouver quand s'arrêter ! le dernier entier à écrire sera b, donc a doit augmenter (a+1) et on s'arrête quand a == b, et là ont fera juste print(a) sans ajouter un espace cette fois, et sans rappeler la fonction.

Tout ces exemples sont différents, et il est dangereux de vouloir imiter la solution d'un exercice pour en résoudre un autre, la plupart du temps ça ne va pas fonctionner.

Ce qu'il faut faire c'est vraiment penser récursif : je fait en premier ceci puis je recommence avec le reste du problème.

entrainez vous SANS CODER

Exercice 1 :

On veux écrire une fonction qui calcule factoriel n (noté en maths : n!)

$fact(n) = 2 \times 3 \dots \times n$

on pourrait songer à commencer par la gauche mais on aura un problème :

$fact(n) = 2 \times ( 3 \times 4 \dots \times n )$

calculer $fact(n) = 2 \times 3 \dots \times n$ n'est pas un problème vraiment similaire au problème initial. Ca y ressemble mais ce n'est pas tout a fait vrai. car ce produit des entiers de 3 à n ne peut pas être écrit comme une factorielle, c'est-a-dire ne peut pas être écrit fact(quelques chose)

Vous l'avez remarqué, on peut souvent prendre le problème par le haut ou par le bas. par exemple :

longueur(txt) = 1 + longueur(txt[1:]) si je vais de gauche à droite (de bas en haut si je regarde l'indice de 0 à n-1)

mais aussi bien :

longueur(txt) = 1 + longueur(txt[;-1]) si je vais de droite à gauche (de haut en bas si je regarde l'indice de n-1 à 0)

dans un cas j'ai retiré le 1er caractère, dans l'autre cas le dernier, les 2 sont possibles.

Dans notre factorielle ça ne fonctionne pas. Mais pouvez vous exprimer la récurrence en partant du haut ?

Short Answer Exercise

$fact(n) = \dots fact(n-1)?$
Que mettez vous à la place des ... ? (mettre la réponse sans espace, et avec un opérateur
Your answer:

Correct!

Exercice 2

Proposez un algorithme récursif de calcul du produit de deux entiers naturels a et b en supposant que les seules opérations de base dont vous disposez sont

la somme de deux entiers a et b : a + b
soustraire 1 à un entier

On va transformer la multiplication en additions : $a \times b = a + a + \dots +a\ (somme\ de\ b\ termes)$

Short Answer Exercise

$produit(a,b) = \dots$
Que mettez vous à la place des ... ? (mettre la réponse comme une formule incluant l'appel de produit.
Ne mettre aucun espace dans la réponse.
Your answer:

Correct!

Exercice 3 : Palindrome

Un palindrome est un mot dont les lettres lues de gauche à droite sont les mêmes que celles lues de droite à gauche.

Les mots radar, elle, été, ici, kayak sont des palindromes.

On veux écrire une fonction qui teste si un mot est un palindrome.

ispalindrome(txt) renvoi True si txt est palindrome et False sinon.

ATTENTION AU TYPE : la fonction renvoie un booléen

le cas général doit donc renvoyer un booléen.

Quand on crée une liste on écrit par exeemple des choses comme :

return [a] + fonction(paramètres)

Dans le cas de booléen ce sera focéement :

return condition1 AND (ou OR) condition2

Vous noterez aussi que si le mot n'a qu'une seule lettre ou aucune lettre, il est forcément un palindrome.

Short Answer Exercise

le texte est un palindrome si ...==...
Ecrire l'expression booléenne qu'il vaut tester.
Your answer:

Correct!

Short Answer Exercise

écrire la seconde condition qui va permettre de continuer l'opération: cette condition est un rappel de ispalindrome avec les bon paramètres.

Le cas général s'écrire donc : return condition1 and condition2
Your answer:

Correct!

Et pour le cas de base, si la chaine est vide ou si la chaine ne contient qu'un caractère, que doit on renvoyer ?

Short Answer Exercise

Si len(txt) <=1 : return...
Your answer:

Correct!

Exercice 4

on veux tester si un lettre apparait dans un mot :

def appartient( lettre:str , mot:str ) -> bool :

Pour le cas général, il sera en deux parties :

On a trouvé la lettre :

Short Answer Exercise

if ... (sans aucun espace)
Your answer:

Correct!

dans ce cas :

Short Answer Exercise

return ... (sans aucun espace)
Your answer:

Correct!

ou bien on ne 'a pas trouvée :

Short Answer Exercise

return ... (sans aucun espace)
Your answer:

Correct!

Mais on pourrait l'écrire en une ligne, avec les même conditions que ci-dessus, mais qu'allez vous écrire entre les deux ?)

Short Answer Exercise

return condition1 ... condition2 (sans aucun espace)
Your answer:

Correct!

T 4.1 Partie 2 : implémenter l'interface

Posted on October 12, 2021 by jlt

Nous avons abordé le concept de Structure de Données Abstraite, et nous avons vu comment, avec un jeu minimal de primitive, nous pouvons manipuler une LISTE.
Rapellons les primitives utilisées :

cree_vide() : création d'une LISTE vide notée []
est_vide(liste) : True si la liste est vide et False sinon
ajouter(x,liste) ajouter un élément en tête
donne_tete(liste) : renvoi la tête
donne_queue(liste) : renvoi la queue qui est aussi une LISTE

A vous de créer cette interface

Commençons par cree_vide(). Ce n'est pas très difficile, cette fonction renvoie simplement une liste vide !

Maintenant la primitive ajouter().

Maintenant la primitive est_vide().

Là encore c'est très simple...

Et pour terminer, donne_tete et donne_queue

Avec la POO

La POO est un moyen très adapté pour créer des interfaces très faciles à utiliser. Vous allez créer une interface assez similaire aux 2 précédentes, mais utilisant le paradigme de la POO.

création d'une liste vide

On va créer une classe Liste. Les objets Liste auront 1 seul attribut, nommé contenu. Lors de l'instanciation, cet attribut prendra la valeur [].

création d'une méthode isempty

Ajoutez dans votre classe (que vous recopierez) une méthode isempty qui renvoie True si la liste est vide et False sinon.

création d'une méthode d'ajout

Pour ajouter des éléments nous n'allons pas créer une méthode ajouter.

En fait nous voudrions ajouter des éléments ainsi :

l1 = Liste() -> l1.contenu = []

l2 = Liste(3, l1) # ajoute 3 dans l1 -> l2.contenu = [3]

l3 = Liste(4, l2) # ajoute 3 dans l2 -> l3.contenu = [4, 3]

l4 = Liste(1, l3) # ajoute 3 dans l3-> l4.contenu = [1, 4, 3]

En mode empilé :
l = Liste(5, Liste(3, Liste(4, Liste() ) ) -> l.contenu = [5, 3, 4]

Cela pose un problème : lors de l'instanciation, on écrit l = Liste() sans arguments, tandis que quand on ajoute un élément, on écrit : l = Liste(x, liste), avec 2 arguments. Or, ces 2 instructions appellent la même fonction : le constructeur __init__.

Donc ce constructeur devrait avoir 0 paramètres si on instancie, et 2 paramètres si on ajoute. Cela est possible, en ajoutant des arguments optionnels ayant une valeur par défaut.

Toutefois, le constructeur ainsi modifié est assez complexe, le voici, vous n'avez pas à l'écrire, mais nous allons le commenter pour le comprendre.

création des getters get_tete et get_queue

Il s'agit de simples getters, vous pouvez les implémenter.

get_tete doit renvoyer contenu[0] si la liste est non vide, et [] sinon
get_queue doit renvoyer contenu[1:] si la liste contient au moins 2 éléments (une tête et une queue non vide) et [] sinon

T 4.1 (a finir) TAD LISTE

Posted on October 11, 2021 by jlt

Autres fonctions (cette partie n'est pas faite)

Coding Exercise: get_tete et get_queue

Implémentez les méthodes get_tete et get_queue puis créez une liste dont la tête sera 4, et la queue sera [5, 6, 1].
Vous afficherez les attributs de la liste en utilisant les getters.

class Liste :
    def __init__(self, tete=None , queue=None) :
        # si tete et queue ne sont pas présents,
        # on initialise les attributs (tete et queue) à None :
        if tete == None and queue == None :
            self.tete = None
            self.queue = None
        # sinon :
        else :
            # si la queue est vide, on met la tete dans la queue
            if queue.isempty() : 
                self.queue = None
                self.tete = tete
            # sinon, on ajoute la tete dans la queue
            else :
                if queue.queue != None :
                    self.queue = [queue.tete] + queue.queue
                else :
                    self.queue = [queue.tete] 
            # puis on met x dans tete :
            self.tete = tete
    def __str__(self) :
        return 'tête :' + str(self.tete) + '\nqueue :' + str(self.queue)
    def isempty(self) : 
        return self.tete==self.queue==None
    def get_tete(self) :
        pass
    def get_queue(self) :
        pass

On peut maintenant construire toutes les fonctions qui nous viennent à l'esprit.
Voici quatre exercices à réaliser ci-dessous, pour implémenter de nouvelles fonctions.
Pour chacun de ces exercices, vous ne pouvez utiliser que les fonctions "primitives" définies précédemment, ou une fonction que vous avez vous-même implémentée dans un des exercices ci-dessous.
Vous ne devez donc pas utiliser les instructions usuelles en python pour le type list, notamment accéder un élément avec ma_liste[0] par exemple.

Pour la réalisation des différentes fonctions, vous n'avez pas le droit d'utiliser len, append et []

exercice 1 :

exercice 2

exercice 3

exercice 4

Coding Exercise: Compléter cette fonction qui doit permettre de savoir si un élément x est dans la liste. Vous ne pouvez utiliser ni len, ni for, ni while


def appartient(x, liste):
    '''
    Cette fonction retourne True si x appartient à liste, et False sinon
    Précondition : x est de n'importe quel type, liste est du type abstrait LISTE
    Postcondition : Cette fonction renvoie un booléen
    Exemples : 
    >>> liste_1 = Vide()
    >>> liste_1 = Liste(1, liste_1)
    >>> liste_1 = Liste(2, liste_1)
    >>> liste_1 = Liste(3, liste_1)
    >>> appartient(4, liste_1)
    False
    >>> appartient(3, liste_1)
    True
    >>> liste_vide = Vide()
    >>> appartient(2, liste_vide)
    False
    '''
# compléter ici

exercice 5

Dans cet exercice, vous ne pouvez utiliser ni len, ni for, ni while, ni in

Coding Exercise: Compléter cette fonction qui doit retourner élément de rang n.

Votre fonction doit renvoyer n hors limite si n n'est le rang d'aucun élément de la liste

def lire_index(n, liste):
    '''
    Cette fonction retourne élément de rang n de liste. 
    On utilise les conventions habituelles : le plus a gauche est de rang 
    0, le suivant de rang 1...
    Si n est plus grand que longueur(liste)-1, ou negatif, la fonction 
    affiche le message :n hors limite et retourne None.
    :param n: n est de type entier.
    :param liste: liste est de type abstrait LISTE
    :returns: le type renvoyé est celui de l élement de rang n. La 
                fonction retourne None si n est hors limite ou si 
                la liste est vide. Elle affiche alors un message 
                explicatif.
    Exemples :
    >>> liste_1 = Vide()
    >>> liste_1 = Liste(1, liste_1)
    >>> liste_1 = Liste(2, liste_1)
    >>> liste_1 = Liste(3, liste_1)
    >>> lire_index(1, liste_1)
    2
    '''
# Compléter ici

T 4.1 (partie 1) TAD Listes

Posted on October 10, 2021 by jlt

introduction

Exemple d'implémentation en Python du type LISTE

Le type abstrait de donnée LISTE

Le langage de programmation Lisp (inventé par John McCarthy en 1958) a été un des premiers langages de programmation à introduire cette notion de liste (Lisp signifie "list processing").

On trouve différentes définitions du type abstrait liste.

Dans ce cours, nous définirons une liste comme une structure de donnée permettant de regrouper des données. C'est une structure linéaire qu'on ne peut parcourir qu'en partant du début. Elle est définie par son interface, c'est à dire l'ensemble des fonctions (méthodes), appelées des primitives qui vont permettre de creer et gérer la liste.

Il y a de nombreuses possibilités pour implémenter ce type abstrait, et on a pas besoin de connaître cette implémentation pour l'utiliser. Il suffit de connaître les spécifications des fonctions primitives, pour pouvoir les utiliser et éventuellement écrire d'autres fonctions.

Attention : ce que nous appelons listes dans ce chapitre n'est pas la même chose que les listes que vous connaissez en python. Il s'agit ici de types abstraits qui n'existent pas nécessairement de façon native dans tous les langages, mais peuvent être implémentés.

Le type abstrait LISTE est différent du type list. Nous le noterons dans ce cours, pour bien le différencier, en majuscules : LISTE.

Pour résumé, une LISTE est composée de :

sa tête (souvent noté car), qui correspond au dernier élément ajouté à la liste (en tête de liste)
et sa queue (souvent noté cdr) qui correspond au reste de la liste.

Écriture d'une liste

La manière dont sont affichées les listes dépend de leur implémentation. Dans ce qui suit nous allons conserver un affichage qui permet de bien visualiser la tête et la queue de la liste. Nous allons voir 3 implémentations différentes du type liste, toutes valables et on pourrait en inventer bien d'autres. Mais nous resteront sur le concept initial de John McCarthy

Nous verrons d'abord un premier exemple, sans POO :

Une liste vide contiendra | None | None | (ni queue ni tête)
Une liste à une seul élément n'a pas de queue mais a une tête : | 2 | None |
Une liste à plusieurs éléments : | 5 | 4 3 2 1 |

Notre type abstrait liste utilise donc des chaines de python pour la représentation, car il en faut bien une.

Un deuxième exemple : toujours sans POO, mais avec une notation différente, plus proche des list de python. Vous devrez construire l'interface pour ce cas.

Un troisième exemple : ave la POO

La POO est un outil très pratique pour modéliser des Listes. Nous pourront ainsi par exemple construire des liste ainsi :

une liste a 1 attribut contenu. Dans le cas d'une liste vide cet arrtibut contiendra []

Dans la littérature, on trouve des présentation très variées, souvent de ce type :

(5 , (4 , (3 , (2, (1,None)))))

mais aussi des présentation plus proche de celle de python :

[ 5 4 3 2 1] ou [5, 4, 3, 2, 1] ou avec des ( ).....

Tout est correct, puisque ce n'est qu'un choix de la façon de représenter un type abstrait. La représentation est plus ou moins lisible, mais les plus simples ne rendent pas toujours bien compte de la façon dont les données sont traitées en mémoire et comment on va y accéder.

Définition : Primitive

Un Type Abstrait de Données (TAD), parfois aussi nommé Structure de Données Abstraite (SDA) est implémenté grâce à un nombre restreint de primitives.
Une primitive est une fonction permettant de manipuler le TAD. Dans certain cas, ce peut être une classe (dans ce cas, c'est la constructeur qui joue le rôle d'une primitive lors de l'instanciation), ou une méthode, mais ça revient au même.

Quand on vous demande d'implémenter le type abstrait liste, la question est incomplète, car les définitions de ce TAD sont très variées. Nous allons dans tout ce cours utiliser un jeu de 5 primitives, ce qui correspond à la définition la plus couramment utilisée.

Créer une liste vide
savoir si une liste est vide (True ou False)
ajouter un élément
prendre la tête de la liste
prendre la queue de la liste

Définition : Interface

L'ensemble des primitive de notre TAD est nommé interface du TAD

Avec cette interface, notre TAD est défini. Bien sur, nous pourront créer d'autres fonctions pour manipuler notre TAD, comme par exemple longueur qui donnera la longueur de la liste, on index qui cherche l'indice d'un élément etc et .... mais ces fonctions devront être implémentées en utilisant les primitives.

Tous les langages modernes, et Python ne fait pas exception, utilisent des listes, souvent différente de ce modèle abstrait, et donc tous ont une implémentation d'un jeu de primitives pour manipuler des conteneurs.

Ces fonctions primitives ne sont pas directement utilisées par le programmeur, qui dispose d'autre syntaxes qui font appel à ces primitives.

un premier exemple

Comprendre le fonctionnement des primitives

Ci dessous nous avons implémenté les 5 primitives. Vous ne pouvez pas voir le code de l'impémentation, mais vous allez utiliser help( ) pour lire leurs documentations.

lisez attentivement les spécifications de chaque primitive, car elles vous permettront de comprendre leur fonctionnement.

A vous d'utiliser cette première interface

A vous maintenant !

Un second exemple

Changeons la notation

Dans le premier exemple nous utilisons une notation assez éloignée de celle à laquelle vous êtes habitués en python. Nous allons utiliser une interface très similaire à la première, mais avec une notation plus simple (mais qui ne permet pas aussi facilement de distinguer tête et queue de la liste).

Comme vous le voyez ici, notre TAD peut assez bien être utilisé pour implémente un type LISTE ressemblant au type list de python. Néanmoins, les liste de python peuvent aussi être utilisée d'autres façon, et ne sont pas limitées aux même usages que notre LISTE.

exercices avec cette interface

Vous vous rendez bien compte que, malgré la ressemblance, ce type LISTE n'est pas le même que le type list de python.

Coding Exercise: Compléter cette fonction qui doit permettre de savoir si un élément x est dans la liste. Vous ne pouvez utiliser ni len, ni for, ni while

def appartient(x, liste):
    '''
    Cette fonction retourne True si x appartient à liste, et False sinon
    Précondition : x est de n'importe quel type, liste est du type abstrait LISTE
    Postcondition : Cette fonction renvoie un booléen
    Exemples : 
    >>> liste_1 = Vide()
    >>> liste_1 = Liste(1, liste_1)
    >>> liste_1 = Liste(2, liste_1)
    >>> liste_1 = Liste(3, liste_1)
    >>> appartient(4, liste_1)
    False
    >>> appartient(3, liste_1)
    True
    >>> liste_vide = Vide()
    >>> appartient(2, liste_vide)
    False
    '''
# compléter ici

cours CI

Posted on October 2, 2021 by jlt

Première partie : les pyBox

I. Les autotests : tester les variables ou les fonctions, aléatoire ou choisi

A) pour tester le contenu d'une variable

[pyBox
slug='auto_a'
title='exemple1'

defaultcode='# ecrire un code qui crée une variable x et lui affecte la valeur 3
votre code ne doit produire aucune sortie en console
'
solver='x=3'
autotests='x'
] Testez avec rien, puis avec x=1 puis avec x=3 dans le code

[/pyBox]

L'autotest génèrera une erreur si la variable x est non définie dans le code élève ou si elle n'a pas la même valeur que lors de l'exécution du solver.

On peut cumuler l'autotest avec une sortie console. par exemple :

[pyBox
slug='auto_a2'
defaultcode='# ecrire un code qui crée une variable x et lui affecte la valeur 3
votre code doit ensuite afficher : x = 3
'
solver='x=3
print("x = ",x)
'
autotests='x'
] Testez avec x=3 dans le code, sans le print, puis avec le print.
[/pyBox]

En plus de l'autotests, les sorties consoles sont testées aussi.

B) pour tester une fonction

C'est ce que j'utilise le plus, sauf début d'année en première (évidement).

[pyBox
slug='auto_b'
defaultcode='def ma_fonction(n:int) -> int:
    # votre code ici
'
solver='def ma_fonction(n):
    return n**2
'
autotests='ma_fonction(3)
ma_fonction(2)
ma_fonction(_rint(3,9))
'
] Ecrire une fonction qui prend en paramètre un entier n et renvoi la valeur de n².

On peut aussi utiliser des balises latex : [latex size=2](\frac{3}{2})^2[/latex]
[/pyBox]

L'autotests va appeler le solver avec les appels définis, et comparer avec les résultats fournis par le code élève pour les mêmes appels.

vous noterez bien la ligne : ma_fonction(_rint(3,9))

_rint est un raccourci pour random.randint et on a pas besoin d'importer random. Ce test sera donc aléatoire, ce qui évite dans certains cas des codes qui affichent ou renvoi la bonne réponse sans faire vraiment le code !

(quoique... j'ai vu un élève faire ça puis m'appeler pour valider, sa boite était verte, mais si on exécutait ça marchait une fois sur 10....)

II. le precode

C'est un code qui sera excuté, aussi bien avant le solver qu'avant le code de l'élève. On peut y mettre des import, des fonctions, des variables.

Les variables et les fonctions qu'on nomme avec un _ : _truc ne seront pas visibles pour l'élèves même à l'exécution.

[pyBox
title="précode"
slug='precode'
precode = 'def afficher(val,name):
print(name,"=",val)
var = 1
_var = _rint(1,100)
'
defaultcode='# votre code doit créer une variable x qui vaut 2
et l\'afficher en utilisant la fonction afficher
Vous afficherez ensuite le contenu de deux variables prédéfinies
dans le précode nommées var et _var
'
solver='x = 2
afficher(x,"x")
afficher(var,"var")
afficher(_var,"_var")
'
autotests='afficher(3,"x")
afficher(_rint(3,9),"valeur aléatoire")
'
]Dans cet exercice on a prédéfini (dans le précode) une fonction afficher(valeur,nom) qui affiche la valeur d\'une variable sous la forme nom = valeur.

Exemple (si x vaut 2) : afficher(x,"x") affichera x = 2


le code définit également deux variables, var et _var, que vous devez afficher de la même façon avec la fonction afficher.
[/pyBox]

Attention : l'autotests exécute les appels, mais ici la fonction ne revoie rien mais affiche en console. Le test sera pris en compte mais via les sorties console.

Notez bien aussi :

Before running your code: We defined a function afficher and var equal to 1.

la variable _var n'est pas montrée, mais elle existe.

III. repeats avec generator : Tests aléatoires

On ajoute un élément generator qui génère une (ou plusieurs) valeur(s) qui sera(ont) utilisée(s) par input().

repeats permet de définir combien de test on va faire, ce n'est intéressant que si le générator contient de l'aléatoire.

Ici j'ai ajouté un taboo et je ne met aucun defaultcode, la boite sera donc vide.

[pyBox
slug='absolute'
title="repeats + generator (quand il y a des input)"
generator="print(_rint(-100, 100))"
repeats=3
solver='print(abs(int(input())))
'
taboo="abs"
] Votre code doit lire (avec input) un nombre entier et afficher la valeur absolue de ce nombre.


CONTRAINTE : Vous ne devez pas utiliser la fonction abs() de python. [/pyBox]

Inconvénient : on ne maitrise pas les tests. Dans l'exemple ci-dessus, il faudrait tester avec un négatif, un positif et avec 0, mais générator ne me permet pas de le faire....

parfois ça peut quand même servir, si on a pas de cas particulier à tester. exemple :

[pyBox
slug='plus_grand'
generator="print(_rint(-100, 100))
print(_rint(-100, 100))"
repeats=3
solver='print( max( int(input()),int(input()) ) )
'
taboo='max'
] Votre code doit lire (avec input) 2 nombres entiers et afficher la valeur du plus grand.


CONTRAINTE : Vous ne devez pas utiliser la fonction max() de python. [/pyBox]

mais même ici, on ne teste pas le cas ou a = b. Si l'élève écrit :

a = int(input())
b = int(input())
if a>b :
   print(a)
if b>a :
   print(b)

dans le cas a = b le code ne produira rien, mais ce cas n'est pas testé et le correcteur dira que c'est correct...

IV. input au lieu de generator+repeats : Tests choisis, pas d'aléatoire

C'est assez similaire mais ici on défini les tests. Inconvénient, je n'arrive pas à mettre un test aléatoire dans ce cas...

[pyBox
slug=′plus_grand_2′
input1="1\n2"
input2="2\n2"
input3="3\n2"
solver='print( max( int(input()),int(input()) ) )
'
taboo='max'
] Votre code doit lire (avec input) 2 nombres entier et afficher la valeur du plus grand.


CONTRAINTE : Vous ne devez pas utiliser la fonction max() de python. [/pyBox]

pyScramble

[pyScramble 
slug="scramble"
solver="a=1\nb=a+1\nc=b+1"
] Arrangez les lignes dans le bon ordre, pour que le code s'exécute sans erreur.[/pyScramble]

V. Des codes utilisant random

Ces codes posent un problème : il faut initialiser le générateur aléatoire dans le solver et dans le code élève de la même façon.

Prenons cet exemple, qui ne fonctionne pas bien :

[pyBox
slug="plus_grand_3"
title="exemple qui ne fonctionne pas…"
generator='print(_rint(3,8))'
repeats=3
solver='a = int(input())
b = _rint(0,10)
print("le plus grand de ",a,"et",b,"est", max(a,b) )
'
taboo='max'
] Votre code doit lire (avec input) 1 nombres entier et afficher la valeur du plus grand entre ce nombre et un autre que vous générez aléatoirement entre 1 et 10.


CONTRAINTE : Vous ne devez pas utiliser la fonction max() de python. [/pyBox]

le code élève correct :

import random
a=int(input())
b = random.randint(0,10)
if a>= b:
   print(a)
else :
   print(b)

Ce code devrait donner la même chose que le solver (même si, dans le solver, je m'autorise _rint() et max() parce que je suis feignant, le taboo c'est seulement pour les élèves...)

En fait il faut initialiser le générateur aléatoire. J'ai tenté ceci : l'initialiser à un nombre fixe dans un précode écrit ainsi :

precode = "import random as _rd
_rd.seed(5)
"

ce qui donne ce pyBox :

[pyBox
slug="plus_grand_4"
title="exemple qui ne fonctionne toujours pas…"
precode = "import random as _rd
_rd.seed(5)
"
generator='print(_rint(3,8))'
repeats=1
solver='a = int(input())
b = _rint(0,10)
print("le plus grand de ",a,"et",b,"est", max(a,b) )
'
taboo='max'
] Votre code doit lire (avec input) 1 nombres entier et afficher la valeur du plus grand entre ce nombre et un autre que vous générez alétoirement entre 1 et 10.


CONTRAINTE : Vous ne devez pas utiliser la fonction max() de python. ][/pyBox]

D'une part, ça ne génère pas vraiment des tests aléatoires, les nombre générés sont toujours les mêmes à chaque exécution. Mais pire, les deux codes (solver et élève) n'obtiennent pas la même chose (il semble donc que precode n'est exécuté qu'une seule fois...)

Il faut donc se résoudre à faire le random.seed dans le code (dans le solver et dans le code élève). Ca perturbe les élèves et on perd du temps.

Depuis peu j'ai choisit de créer dans le précode une fonction d'initalisation :

precode = "import random as _rd
def _initialisation_exercice():
   _rd.seed(_codeInitRandom)
_codeInitRandom = _rint(3,10)
"

je génère un nombre aléatoire caché _codeInitRandom qui sera bien le même dans les deux codes. j'appelle dans les deux code la fonction initialisation_exercice() que je met dans le defaultcode évidement...

exemple :

[pyBox
slug="plus_grand_5"
title="et finalement, je contourne le problème"
precode = "import random as _rd
def _initialisation_exercice():
    _rd.seed(_codeInitRandom)

_codeInitRandom = _rint(3,10)
"
generator='print(_rint(3,8))'
repeats=3
solver='_rd.seed(_codeInitRandom)
a = int(input())
b = _rint(0,10)
print("le plus grand de ",a,"et",b,"est", max(a,b) )
'
defaultcode='#La ligne ci-dessous est requise pour la validation automatique, laissez là mais ignorez la
_initialisation_exercice()
import random
'
taboo='max'
] Votre code doit lire (avec input) 1 nombres entier et afficher la valeur du plus grand entre ce nombre et un autre que vous générez alétoirement entre 1 et 10.


CONTRAINTE : Vous ne devez pas utiliser la fonction max() de python. [/pyBox]

Notez bien que la fonction et le code d'initialisation sont cachés, cela évite des affichages inutiles lorsque l'élève exécute le code.

De même j'ai importé random as _rd. Le import random est donc indispable dans le code élève. (ici je l'ai mis dans le defaultcode mais je pourrais ne pas le mettre...)

SOS la boite ou même tout le collapsible ne s'affiche plus

La cause la plus fréquente est un problème de guillements.

Par exemple :

[pyBox
slug="bidon"
defaultcode="def ma_fct():
   """
   docstring
   """
   # faire afficher hello
"
solver="def ma_fct():
   """
   docstring
   """
   print('hello')
"]L'énoncé[/pyBox]

Dans ce cas vous pouvez avoir un message d'erreur, ou bien un affichage incomplet (dans l'exemple ci-dessus, le defaultcode ne s'affiche pas bien).

Mais testez. Remplacez le code par un code valide, par exemple mettez pass dans la fonction et exécutez.... vous obtenez une boite jaune avec ce message :

PyBox error: unknown option docstring

Il a voulu exécuter le solver, mais il ne l'a pas trouvé. Le default code c'est arrété aux " puis il a lu "" dont il ne fait rien, puis le mot docstring, qu'il ne comprend pas....

Pour éviter cela, il vaut mieux utiliser des ' plutot que " pour délimiter les codes, puis des " dans le code :

[pyBox
slug='bidon'
defaultcode = 'def ma_fct():
   """
   docstring
   """
   # faire afficher hello
'
solver = 'def ma_fct():
   """
   docstring
   """ 
   print("hello")
'
]L'enoncé[/pyBox]

Mais même ainsi il vous arrivera cela :

[pyBox
slug='bidon'
defaultcode = 'def ma_fct():
   """
   docstring
   """
   # faire afficher l'expression hello
'
solver = 'def ma_fct():
   """
   docstring
   """ 
   print("hello")
'
]L'enoncé[/pyBox]

je ne vous montre pas ce que ça donne car ça met un gros bordel.... Le [/pyBox] n'a pas été lu, et du coup votre boite pyBox reste ouverte jusqu'à ce qu'on rencontre un /pyBox.... qui se trouvera dans un autre exo et tout sera fusionné en une seule boite plus ou moins lisible (plutot moins que plus).

bref, vous n'y comprendrez rien, et c'est juste que vous avez oublié d'échapper l'apostrophe.

plus vicieux, l'oubli d'un <

[pyBox
slug="bidon2"
defaultcode="
"
solver="if 3 < 2:
   print(a)
"]
[/pyBox]

la boite ne s'est purement et simplement pas affichée.... le comportement peut être variable mais il y aura forcément souci.

Rectifions :

[pyBox
slug="bidon2"
defaultcode="
"
solver="if 3 &lt; 2:
   print(a)
"]
[/pyBox]

Les comportements peuvent varier suivant le contexte, l'oubli d'échappement d'une apostrophe peut impliquer la non lecture d'un [/collapsible] et du coup plus rien ne s'affiche, ou ne s'affiche pas dans le collapsible ou je ne sais quels effets les plus déroutants qui soient...

bref....

Quand ça ne marche pas regardez bien vos " et vos ', pensez aussi aux <, et sinon il reste la possibilité d'un code trop long, il y a une limite à chaque code et à la boite totale.

Deuxième partie : les pyHint pyWarn images latex etc...

pyHint

le pyHint peut figure dans le texte d'un exercice ou seul, dans une boite html personalisé comme un pyBox.

exemple si on met seul :

[pyHint hint="Aide"]le texte de l'aide [/pyHint]

Aide

et dans un pyBox :

[pyBox
slug='blabla'
solver='le code'
]L'enoncer de l'exercice.<br>
[pyHint hint="Aide"]le texte de l'aide [/pyHint]
[/pyBox]

pyWarn

[pyWarn]le texte du warning [/pyWarn]

le texte du warning

comme pyHint, pyWarn peut s'utiliser dans un pyBox.

images

Lorsque vous ajoutez un bloc image vous obtenez ceci :

vous pouvez televerser une image depuis votre ordi, elle sera visible et en même temps, ajoutée à la bibliothèque.

Vous pouvez aussi choisir une image de la bibliothèque, ou un lien vers une image.

Pour insérer une image dans un pyBox :

commencez par ajouter un bloc image, et mettez votre image. Puis convertissez ce bloc en html et copiez le code html, qui doit ressembler à ça :

<figure class="wp-block-image size-large">
<img src="https://cscircles.cemc.uwaterloo.ca/wp-content/uploads/img-CI.jpg" alt="" class="wp-image-15151"/>
</figure>

que vous collez dans l'énoncé de votre exercice. Vous supprimerez ensuite le bloc image.

latex

comme les pyWarn et pyHint le code latex peut être inséré dans l'énoncé d'un pyBox ou pyExample, ou dans un paragraphe.

[latex size=2]\sum\limits_{j=1}^k A_{\alpha_j}[/latex]

$\sum\limits_{j=1}^k A_{\alpha_j}$

Lektionen für junge Schülerinnen und Schüler

Posted on September 26, 2021 by pyter

kurze Info zur Gruppe

Die Übungen sind für jüngere Schülerinnen und Schüler die an der Informatik-AG teilnehmen und für die die Übungen teilweise noch nicht bekannte mathematische Sachverhalte verwenden - sie lehnen sich daher an Übungen aus dem normalen Kursprogramm an

Angelehnt an die Übung zu milkTaxes aus Abschnitt 1E - Fehler. Lies dir auf jeden Fall einmal den Hinweis (Hint) durch!

T 3.4 Parcours récursifs d'itérables

Posted on September 25, 2021 by jlt

Le Triptique CAC

Dans tous les algorithmes que vous avez rencontrés, certaines techniques reviennent souvent. Notamment l'utilisation de :

Ccompteur : exemple : compter les valeurs paires dans une liste
Aaccumulateur : exemple : faire la somme des éléments d'une liste
Ccurseur : exemple : rechercher le max des valeurs d'une liste ou rechercher l'indice du max (ce n'est pas tout à fait la même chose)

Vous avez appris à manier ces outils dans des contextes variés. Parfois il faut utiliser deux de ces techniques en même temps.
Par exemple, calculer la moyenne des valeurs paires d'une liste demande un compteur (pour compter les valeurs paires) et un accumulateur (pour additionner les valeurs paires), et on renvoie le rapport somme des valeurs / nombre de valeurs

Dans les cours précédents vous avez appris à utiliser la récursion. Ici nous allons l'appliquer à des itérables (listes, chaîne de caractères etc...)

Transposons ces notions en récursif (pour des parcours de listes)

compteur récursif

Reprenons un exemple de Compteur en impératif: compter le nombre de valeurs paires d'une liste.

Comment faire la même chose en mode récursif

Notre compteur nbMult2 dans la fonction nbrePairs(lst) peut se concevoir de façon récursive comme :
nbMult2 = (1 si l[0] est pair, 0 sinon) + nbrePairs du reste de la liste
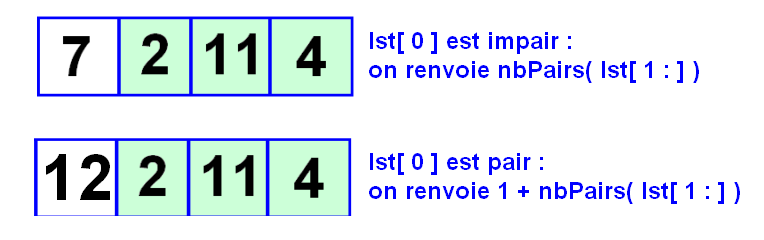
Si le 1er nombre est pair on renvoie 1 + nombre pair du reste
Si le 1er nombre est impair on renvoie 0 + nombre pair du reste

Par exemple : nb=nbPairs([1, 2, 3, 4, 6]) :

renvoyer 0 + nbPairs([2, 3, 4, 6])................................. # 0 car 1 est impair
renvoyer 0 + (1 + nbPairs(3, 4, 6]) )...............................# 1 car 2 est pair
renvoyer 0 + (1+ ( 0 + nbPairs([4, 6]) )........................# 0 car 3 est impair
renvoyer 0 + (1+ ( 0 + 1 nbPairs([6]) ) ) ) ................. # 1 car 4 est pair
renvoyer 0 + (1+ ( 0 + ( 1 + ( 1 + ( nbPairs([]) ) ) ) ).. # 1 car 6 est pair
renvoyer 0 + (1+ ( 0 + ( 1 + ( 1 + ( 0 ) ) ) ).. # fin, on appelle plus la fonction !

Et quand il n'y a aucun élément (liste vide) : nbPairs([]) = 0

La longueur de la liste décroit, la liste finira par être vide
le nombre d'élément pairs es bien égal à ce qu'on renvoie

La condition d'arrêt : si lst est vide, nb=0, s'écrit :

if len(lst) == 0:
    return 0

Exercices avec un compteur

Accumulateur récursif

Les accumulateurs et la récursion

Reprenons un exemple d'accumulateur en impératif : calculer la somme des éléments d'une liste

Notre fonction somme(lst) ci-dessus se comprend de façon récursive comme :

somme = lst[0] + somme du reste de la liste = lst[0] + ( lst[1] + somme du reste ) = etc...

jusqu'à ce que le reste ne contienne aucun élément (liste vide) et la somme sera alors 0.

Exemple :

 somme = somme([2, 4, 1, 5]) 
       = 2 + somme([4, 1, 5])
       = 2 + (4 + somme([1, 5]) ) 
       = 2 + (4 + (1 + somme([5]) ) )
       = 2 + (4 + (1 + (5 + somme([]) ) ) )
       = 2 + (4 + (1 + (5 + 0) ) ) ) = 10

le cas de base sera : si la liste est vide, renvoyer 0

Assurément :

La liste perd un élément à chaque appel, elle finira par être vide
somme(tous les éléments) est bien égal à lst[0] + sommes des autres éléments

Exercice

Codez la fonction somme en récursif

Regardez bien ce que nous avons écrit :
somme = lst[0] + somme du reste devient, dans python :

return lst[0] + somme(lst[1:])

Et pour la condition d'arrêt :
jusqu'à ce que le reste ne contienne aucun élément s'écrit :

if len(lst) == 0 :
    return 0

Des coûts cachés...

Dans les exemples que nous avons traité, nous avons utilisé le slicing avec des instructions comme :

somme(lst[1:])

Pour exécuter une telle instruction, l'interpréteur python va dupliquer la liste (sauf le premier élément). La complexité de cette opération est O(n). Si cette opération doit être réalisé à chaque appel et qu'on fait N appels, on se retrouve avec une complexité en O(n²) alors qu'on a un algorithme en O(n). C'est donc bien commode mais plutôt désastreux.

Nous allons voir comment éviter ces copies de lites, donc coder sans slicing.

Commençons par un exemple.

On veux écrire une fonction estTriee(lst) qui renvoie True si la liste est triée (croissante) et False sinon.

Une version impérative pourrait être :

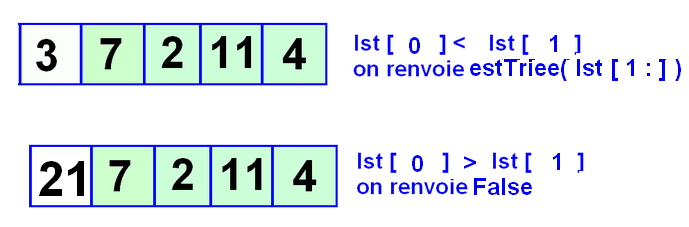
Ce problème est clairement récursif. On compare 2 éléments (on commence par les 2 permiers) et on vérifie l'ordre. Si l'ordre est mauvais on renvoie False, sinon au continue sur le reste de la liste.

Il n'y a pas à proprement parler de curseur dans cette fonction, mais la technique reste quand même assez similaire. Une variante serait de renvoyer la position du premier élément non ordonné, et on aurait vraiment un curseur. Mais nous allons rester sur la version plus simple donnée ci-dessus..

1ere version : en utilisant des slices, pour découper la partie de liste restant à traiter.

Ce code fonctionne et il est assez similaire à la version non récursive.

L'algorithme est clairement de complexité linéraire (n-1 comparaison)

Mais notre code n'est pas de complexité linéaire ! En effet, à chaque exécution de estTriee, on effectue une copie de lst.

Pour une longueur N, je dois rappeler estTriee avec une longueur n-1, et je dois copier n-1 élément dans une nouvelle liste. Le temps d'éxécution peut s'ecrire :

T(n) = T-1) + T(n-1) + n

Pour comprendre cette formule, prenons une analogie :

Je dois éplucher n pommes de terre. Le temps que je vais mettre est en principe égal au temps d'éplucher une pomme de terre + le temps d'éplucher les n-1 restantes.

T(n) = T(1) + T(n-1) nous donne une complexité linéaire

Mais imaginons que après chaque pomme de terre épluchée, je doive déplacer une à une toutes les pommes de terre restantes dans une autre pièce avant de poursuivre l'épluchage...

Le temps total sera alors :

T(n) = T(1) + T(déplacer une a une) + T(n-1)

Et comme je dois toutes les déplacer, le temps de déplacement sera proportionnel à n -1. Notons T' le temps pour déplacer une pomme de terre :

T(n) = T(1) + (n - 1) T' + T(n - 1)

Et donc

T(n) = T(1) + (n-1) T' + [  T(1) + (n-2) T' + T(n-2) ]
     = 2 . T(1) + [(n-1) + (n-2)] T' + T(n-2)
     = 2 . T(1) + [(n-1) + (n-2)] T' + [  T(1) + (n-3) T' + T(n-3) ]                      
     = 3 . T(1) + [(n-1) + (n-2) + (n-3)] T' + T(n-3)

Etc.... on arrivera à :

T(N) = N . T(1) + (1 + 2 + ... + n-1) T'

et on reconnait la somme $\sum\limits_{n = 1}^{N-1} n = \frac{N(N-1)}{2} = 0(N^2)$

Cette formule de récurrence mène donc à une complexité en O(n²).

Retenir :

Si le cas général est en temps constant : T(N) = O(1) + T(N-1) -> complexité linéaire O(N)

Si le cas général est en temps proportionel à N: T(N) = O(N) + T(N-1) -> complexité quadratique O(N²)

Comment éviter le slicing ?

Pour éviter le slicing, il va falloir utiliser les indices. En impératif, nous disposons de l'itérateur qui parcours aisément la liste. En récursif c'est plus délicat, et pour y parvenir nous allons devoir ajouter un attribut à notre fonction.

Au départ il vaudra 0, et nous allons lui attribuer cette valeur par défaut.

A chaque appel de estTriee( lst, n )

on compare lst[n] à lst[n+1]
- Si les deux valeur sont dans l'ordre on reprend en incrémentant n
- sinon on renvoie False :

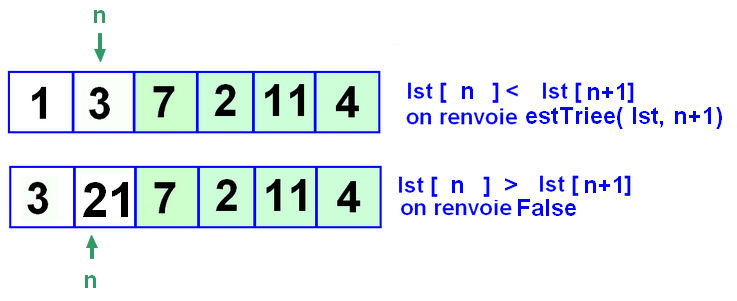
On s'arrêtera au dernier, qu'on aura pas besoin de comparer au suivant puisqu'il n'y a plus de suivant.

Le cas de base est donc : si n = len(lst) - 1 renvoyer True

Ici le cas général et constitué d'un simple test de comparaison, une affectation, et un appel, c'est bien en temps constant : T(N) = T(1) + T(N-1)

La complexité du code est donc linéaire O(N).

Retenir :

Pour connaitre l'indice de l'élément en cours de traitement :

° Définir un paramètre avec valeur par défaut égale à 0

° A chaque appel, incrémenter ce paramètre

Exercices

Reprendre les 2 codes des accumulateurs et les réécrire en n'utilisant pas de slice.

Somme des éléments d'une liste

Nombre d'élément pairs dans une liste

Si vous n'aimez pas les paramètres par défaut....

Il existe une autre façon de procéder. L'idée est la même : ajouter un paramètre. Mais au lieu d'en ajouter un avec une valeur par défaut, on crée purement et simplement une autre fonction :

Example

Détermine (en récursif et sans slice) si une liste est triée ou non

def estTriee(lst: list ) -> bool:
   """
   :param: lst de type list : liste de nombres entiers
   :returns: True si la liste est triée croissante, False sinon.
   """
   return estTrieeRec(lst, 0)

def estTrieeRec(lst, n):
   """
   :param: lst de type list : liste de nombres entiers
   :param n: indice de l'élément qu'on doit comparer lors de cet appel
   :returns: True si la liste est triée croissante, False sinon.
   """
   if len(lst) - 1 == n: 
        # on est au dernier élément, la liste est donc triée
        return True
   if lst[n] < lst[n+1]:
       # les éléments sont dans l'ordre, on passe au suivant
       return estTrieeRec(lst, n+1)
   else :
       return False

print(estTriee([1, 2, 3, 4]))
print(estTriee([1, 2, 3, 1]))

RETENIR

Le problème des traitements récursifs d'itérables est un peu différent, on ne dispose pas d'un itérateur comme dans la boucle for, et pourtant on itère...

1er solution : on fait du slicing
exemple :

def somme_lst(lst) :   
     if len(lst) == 0 : 
         return 0    
     return lst[0]  + somme_lst(lst[1:])

C'est plutot simple, et élégant, mais cela à un coût ( en 0(n) ) et c'est donc peu recommandé d'autant plus si on prend aussi en compte la complexité en espace.

2eme solution : un paramètre par défaut (ou plusieurs)

exemple :

def somme_lst(lst, n = 0) :
    if n == len(lst) : 
        return 0
    return lst[n]  + somme_lst(lst, n+1)

3eme solution : une fonction intermédiaire ou une fonction locale

exemple

def somme_lst(lst ) :
    return somme_lst_rec(lst, 0)

def somme_lst_rec(lst, n) :
    if n == len(lst) : 
        return 0
    return lst[n]  + somme_lst_rec(lst, n+1)

variante avec fonction locale :
def somme_lst(lst) :
    def somme_lst_rec(lst, n):
        if n == len(lst): 
            return 0 
        return lst[n]  + somme_lst_rec(lst, n+1)
    return somme_lst_rec(lst, 0)

Curseur récursif 1 : la fonction getMax

Les curseurs sont utilisés lorsqu'on doit scanner un itérables pour repérer un éléments selon un critère. Par exemple le plus grand, ou la dernière (ou première) occurrence d'une valeur, ou le premier (ou dernier) multiple d'un nombre, ou une clef d'un dictionnaire ayant une valeur donnée etc...

Les codes sont présentés pour une recherche du max mais peuvent aisément être adaptés pour la recherche du min.

Recherche du max : on déplace le curseur en notant la valeur la plus grande

Avant de débuter notons que rechercher le max dans une liste vide n'a pas de sens. Nous ne considérerons que des listes non vides

La version itérative :

on initialise vmax à lst[0]
Du 1er au dernier élément :
- si l'élément est plus grand on actualise vmax

Les curseurs et la récursion

Envisageons un exemple : la recherche de la plus grande valeur dans une liste de nombres : lst = [1, 3, 7, 2, 11, 4] le max est 11.

Si on pense en récursif ici, cela donne :

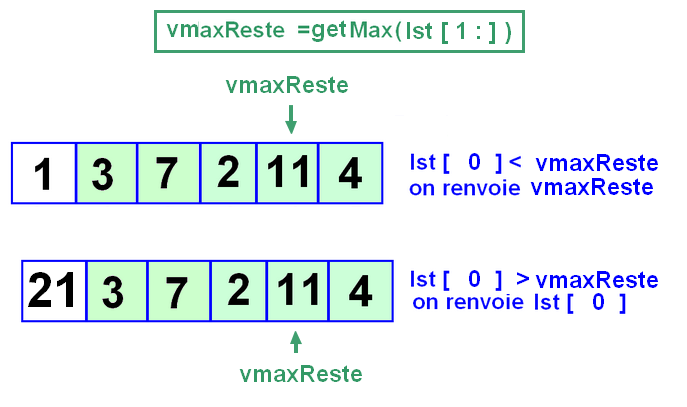
Dans ce code, nous avons écrit :

       vmaxReste  = getMax(lst[1:])
       if lst[0] >vmaxReste:
           vmax = lst[0] 
       else :
           vmax = vmaxReste
       return vmax

Nous avons donc d'abord appelé getMax avant de renvoyer la bonne valeur. Pourquoi ?
On aurait put écrire : :

if lst[0] > getMax(lst[1:])
       return lst[0]
else :
       return getMax(lst[1:])

Mais quel problème cela pose-t-il ?
Pour vous aider, visualiser le code qui a été recopié ci-dessous, puis comparer en visualisant également le code précédant.
N'oubliez pas de choisir la langue anglaise.

Et pour le faire sans slice ?

On introduit un second paramètre, dont la valeur par défaut est 0, qui est l'indice de l'élément en cours de traitement.

Par exemple, si n = 1 :

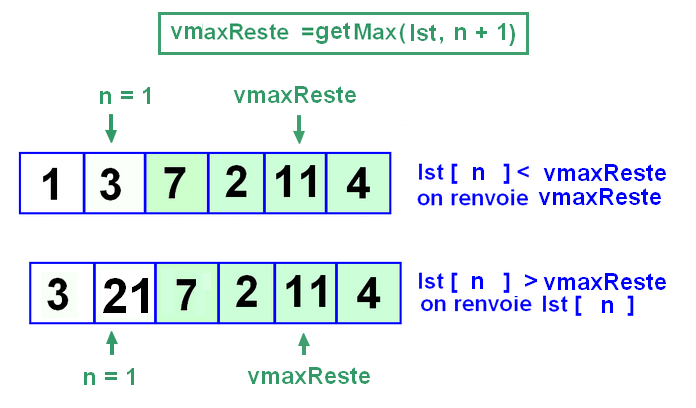
Et le cas de base sera n = len(lst) - 1 : un seul élément donc c'est lui le max, on renvoie lst[n]

Curseur récursif 2 : la fonction idxMax

Cas de la recherche de l'indice du max : on déplace le curseur en notant l'indice

Dans le cas ou l'on recherche l'indice du max de façon récursive, nous allons devoir bien comprendre un point plus délicat : l'indice d'une valeur dans lst[1:] n'est pas le même que l'indice de la même valeur dans lst.

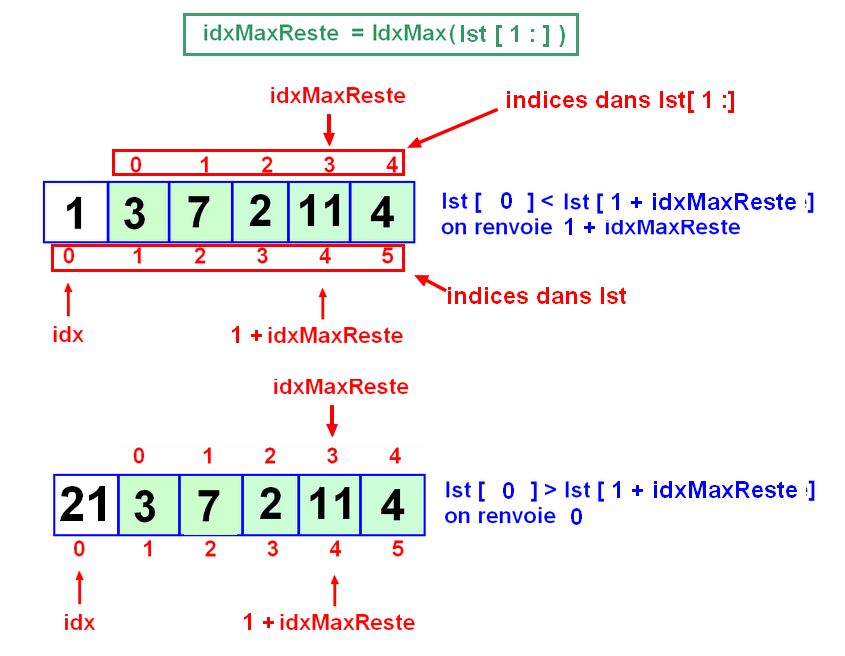
Ce qu'il faut bien comprend c'est le 1 + indice du max du reste.

La fonction s'écrira donc :

la ligne clé est :

        idxMaxReste = 1 + idxMax(l[1:])

L'utilisation du curseur est donc un peu plus compliquée à bien comprendre. En fait, idx est l'indice du max dans la liste, mais dans la fonction appelante, qui contient un élément de plus en tête, l'indice est idx + 1. Une fois bien compris ceci, l'utilisation de curseur ne devrait plus vous poser de difficulté.
La condition d'arrêt si len(l) == 1 : return 0 est intuitive

Une autre approche : un argument supplémentaire par défaut

Dans ces situations, comme pour le cas de la fonction estTriee, une autre approche peut se révéler plus intuitive, mais elle nécessite l'utilisation d'un paramètre supplémentaire qui doit avoir une valeur par défaut.

Rappelons le principe d'un paramètre avec valeur par défaut :

def f(x, n = 0):
    pass
# appel sans le second paramètre :
f(2) # x vaudra 2 et n vaudra 0
f(2) est identique à f(2,0) ou f(2, n=0 )

# appel avec 2 paramètres :
f(2, 3) ou f(2, n=3) # x vaudra 2 et n vaudra 3

La fonction sera définie ainsi :

def idxMax(lst: list, idx = 0)

Exemple : chercher l'indice du max dans [ 1 , 3 , 4 , 2 ]

1er appel : getIdxMax( [1 , 3 , 4 , 2 ] )

idx vaut 0 : on cherche dans toute la liste

On renvoie le plus grand entre lst[0] et getIdxMax(lst, 1)

2ème appel idx vaut 1, On renvoie l'indice associé à la plusgrande valeur (on compare lst[1] et lst[ getIdxMax(lst, 2) ]

Voir ci-dessous, par exemple un appel avec idx = 2 :

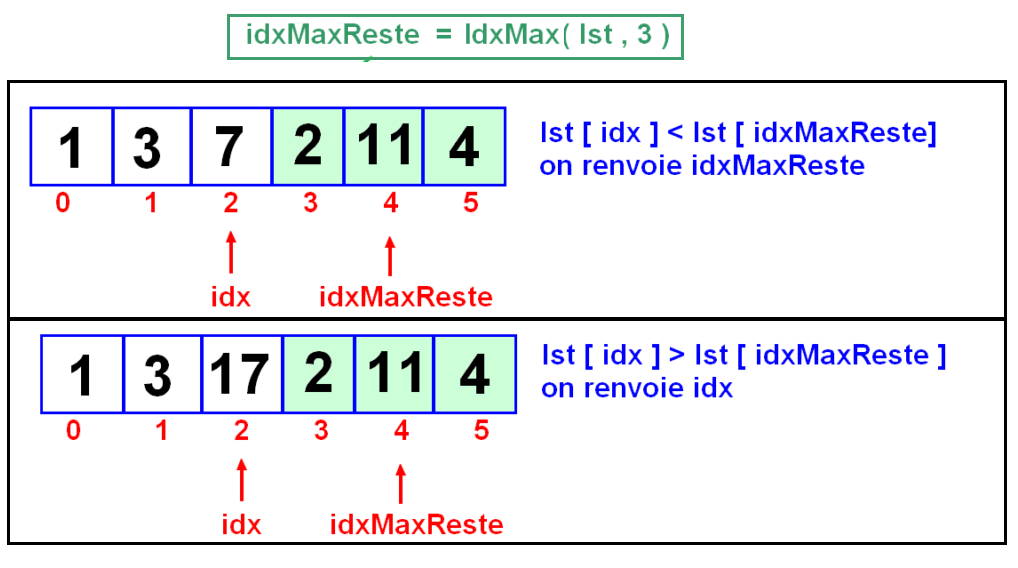
etc... et on arrête quand idx et l'indice du dernier élément, c'est-à-dire len(lst) - 1. Dans ce cas l'indice du max est idx puisqu'on ne cherche que parmi le dernier élément.

L'algorithme peut être décrit ainsi :

cas général :
idxMaxReste = indice_du_max(lst, idx + 1) (indice du plus grand dans le reste de la liste)
on renvoie idx si lst[idx] > lst[idxMaxReste] sinon on renvoie idxMaxReste
cas de base :
si idx est l'indice du dernier, il n'y a pas de reste de la liste. On renvoie idx

On se rend compte que les curseur récursifs sans slice sont bien plus simple qu'avec slice, et même plus naturel que la version itérative.

A vous :

Les deux versions de ce code ne sont pas du tout équivalentes. La première utilise des slices lors de l'appel avec lst[1:]. Cela induit des coûts importants de temps de calculs et de coût en mémoire, car python va dupliquer la liste.

La seconde version utilise l'indice et ne requiert aucune copie de liste. Elle sera bien plus efficace en temps et en espace.

Exercice

On vous demande de coder une version récursive de la fonction appartient donnée ci-dessous :

1ère version : avec slicing:

2ème version : Sans slicing (paramètre par défaut ou fonction intermédiaire) :

3 Übungen

Posted on March 23, 2021 by HerrL

Achtung: Manchmal müsst Ihr nur eine Funktion und den oder die Rückgabewerte definieren. Eine Ein- oder Ausgabe ist dann nicht nötig. In anderen Fällen wird eine Ausgabe erwartet. Achtet also auf die Formulierung in der Aufgabenstellung.

le texte pour aider les élèves

Aide

Versuche den Code laut durchzulesen. Dies wird manchmal Gummientchen-debugging genannt.

Arbeite mit range(start, stop, step)

a, b = b, a vertauscht die Inhalte von a und b

Über die Elemente iteriert man mit for lmnt in Liste:

Arbeite mit einer zweiten Liste oder zwei verschachtelten Schleifen.