11C: Geometrie

Lektion 11 hat drei Teile A, B und C, die in beliebiger Reihenfolge beendet werden können.

In dieser Übung werden wir vier Funktionen schreiben, die geometrische Berechnungen ausführen können:

  • eine Funktion, um die Länge der Hypotenuse eines rechteckigen Dreiecks zu berechnen,
  • eine Funktion, um den Umfang eines rechteckigen Dreiecks zu berechnen,
  • eine Funktion, um den Abstand zwischen zwei Punkten in einem zweidimensionalen Raum zu berechnen,
  • und eine Funktion, um den Umfang eines beliebigen Dreiecks zu berechnen.

Hypotenuse

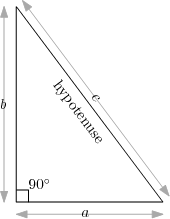Ein rechtwinkliges Dreieck kannst du im Bild auf der rechten Seite sehen. Definitionsgemäß ist einer der Winkel eines rechtwinkligen Dreiecks gleich 90 Grad (ein rechter Winkel). Das Dreieck hat drei Seiten. Die dem rechten Winkel gegenüberliegende Seite hat einen besonderen Namen: man nennt sie die Hypotenuse.

Wie man im Diagramm sieht, sollen a und b die Länge der Seiten, die am rechten Winkel anliegen, bezeichnen, und c soll die Länge der Hypotenuse bezeichnen. Der berühmte Satz des Pythagoras sagt uns, dass

\displaystyle{a^2+b^2=c^2}

Bei der ersten Aufgabenstellung musst du diesen Satz in eine Funktion umwandeln, die, wenn a und b gegeben sind, die Länge der Hypotenuse berechnet.

Programmierübung: Hypotenuse
Definiere eine Funktion hypotenuse(a, b), die die Länge der Hypotenuse c zurückgibt, wenn die anderen beiden Seiten die Längen a und b haben Tipp
Gib Testbefehle wie print(meinefunktion("Test-Argument")) unten ein.

Umfang

Erinnere dich daran, dass der Umfang eines Dreiecks die Summe seiner Seiten ist. So hat der Umfang im obigen Diagramm die Länge a+b+c. Dein Programm sollte annehmen, dass eine korrekte Version von  hypotenuse bereits definiert wurde (du musst sie nicht von der ersten Box zur zweiten kopieren).

Programmierübung: Die Dreiecke sind rechteckig
Definiere eine Funktion rightTrianglePerimeter(a, b), die die Länge des Umfangs eines rechtwinkligen Dreieck ausgibt. Die nicht-Hypotenusenseiten (Katheten) haben die Längen  a und  b; verwende hypotenuse(a, b).
Gib Testbefehle wie print(meinefunktion("Test-Argument")) unten ein.

Abstand im zweidimensionalen Raum

Um über Punkte zu sprechen, die in zwei Dimensionen existieren, verwenden wir zwei Koordinaten (Kartesisches Koordinatensystem), die x Koordinate und die y Koordinate. Wir möchten eine Funktion schreiben, deren Input ein Punktepaar ist und deren Output der Abstand zwischen diesen zwei Punkten ist. Es stellt sich heraus, dass die hypotenuse Funktion uns dabei hilft, diese Aufgabe zu erledigen!

Um mehr ins Detail zu gehen, lass uns annehmen, dass der erste Punkte die Koordinaten (x1, y1) hat, bei denen x1 und y1 reale Zahlen sind, und lass uns annehmen, dass der zweite Punkt die Koordinaten (x2, y2) hat. Die Schlüsselidee ist es, das rechtwinklige Dreieck zu zeichnen, das im Diagramm unten gezeigt wird: die Hypotenuse geht von (x1, y1) zu (x2, y2) und somit entspricht ihre Länge dem Abstand zwischen diesen zwei Punkten.

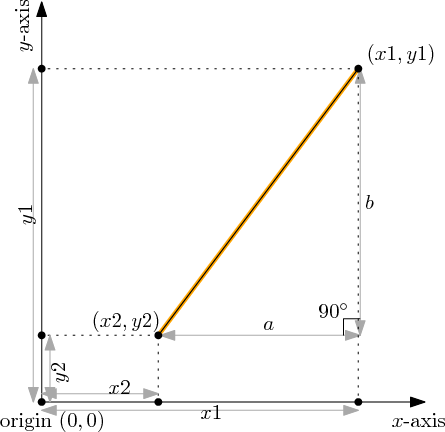
Um die Länge der Hypotenuse zu berechnen, müssen wir die Länge der anderen beiden Seiten des Dreiecks ausrechnen. Dies kann gemacht werden, indem wir die Definition von Koordinaten verwenden (siehe Diagramm):  die horizontale Verschiebung ist a = x1-x2 und die vertikale ist b = y1-y2.

Programmierübung: 2D Distance
Nimm an, dass hypotenuse(a, b) bereits definiert wurde. Definiere eine Funktion distance2D(x1, y1, x2, y2), die den Abstand (distance) zwischen Punkt (x1, y1) und Punkt (x2, y2) berechnet.
Gib Testbefehle wie print(meinefunktion("Test-Argument")) unten ein.

Umfang eines beliebigen Dreiecks

Wir haben jetzt die letzte Übung vor uns. Erinnere dich daran, dass der Umfang die Summe der drei Seitenlängen des Dreiecks ist und beachte, dass die Seitenlänge die gleiche ist, wie der Abstand zwischen zwei Punkten des Dreiecks.

Programmierübung: Secure the Perimeter
Nimm an, dass distance2D(x1, y1, x2, y2) bereits definiert wurde. Definiere nun eine Funktion trianglePerimeter(xA, yA, xB, yB, xC, yC) , die den Umfang eines Dreiecks berechnet, dessen drei Punkte (xA, yA), (xB, yB) und (xC, yC) sind.
Gib Testbefehle wie print(meinefunktion("Test-Argument")) unten ein.

Du bist jetzt für die nächste Lektion bereit!