Comme les autres structures de données, nous avons souvent besoin de parcourir un graphe.
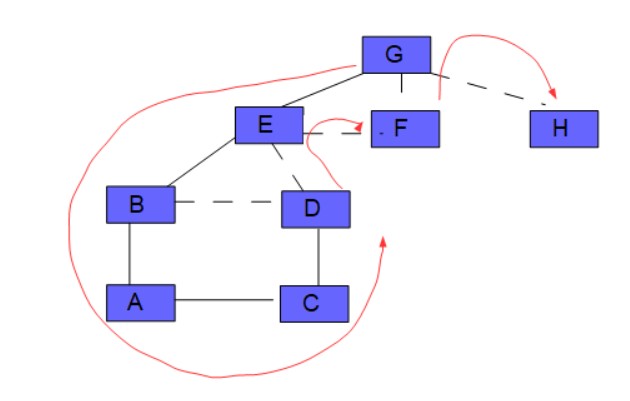
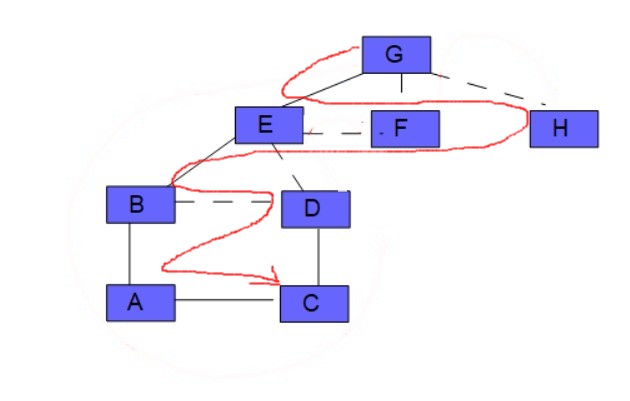
Ci-contre un graphe non orienté, contenant 8 sommets et 10 arrêtes.
Sa matrice d'adjacence se définit ainsi :
matrice = [[0,1,1,0,0,0,0,0], [1,0,0,1,1,0,0,0], [1,0,0,1,0,0,0,0], [0,1,1,0,1,0,0,0], [0,1,0,1,0,1,1,0], [0,0,0,0,1,0,1,0], [0,0,0,0,1,1,0,1], [0,0,0,0,0,0,1,0]]
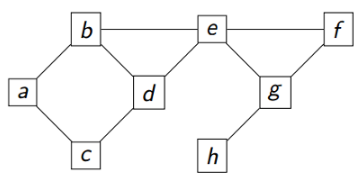
A : B,C
B : A,D,E
C : A,D
D : B,C,E
E : B,D,F,G
F : E,G
G : E,F,H
Deux stratégies possibles
- Recherche en profondeur d'abord, nommée Depth First Search alias DFS
- Recherche en largeur d'abord, nommé BFS, Breadth First Seard, alias BFS
ci-dessous le sujet (à compléter) au format pdf
https://cscircles.cemc.uwaterloo.ca/wp-content/uploads/deroule-dfs-nonrec.pdf
Activité débranchée : Recherche en profondeur d'abord
Pour parcourir le graphes en profondeur d'abord :
- on commence avec un nœud donné (point de départ)
- on explore chaque branche complètement avant de passer à la suivante. Autrement dit, on commence d'abord par aller le plus profond possible. Comme pour les arbres, cet algorithme s'écrit naturellement de manière récursive.
Donc, parcourir un graphe en profondeur à partir d’un sommet, consiste à explorer le graphe en suivant un chemin. Lorsqu’on arrive sur un sommet qui n’a plus de voisins non visités, on remonte dans le chemin pour explorer les voisins non visités d’un autre sommet…
Première version : non récursive
On utilise une pile (aVoir) et une liste (vus)
Prenons en exemple le graphe montré plus haut :
On dispose
- d’un graphe
- d'une liste vus sommets_visités
- et d’une pile aVoir des sommets à visiter
Algorithme de parcours DFS
- Le sommet de départ est par exemple ’G’ on ajoute ce sommet de départ dans vus
- On met dans la pile aVoir tous les voisins de G
- Puis, tant que aVoir n’est pas vide :
• On récupère le sommet de la pile aVoir dans une variable sommet et on ajoute sommet dans vus
• on empile tous les voisins (non déjà visités et non déjà à voir) de sommet dans aVoir
Voici les contenus des variables au premier tour de la boucle tant que :
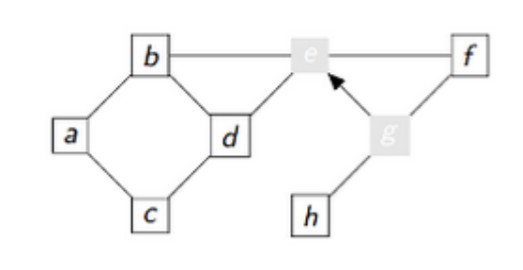
Au début:
sommet = g
aVoir: [h,f,e]
1er tour de la boucle :
sommet=e
vus : [g,e]
aVoir = [h,f,d,b]
Au second tour de la boucle tant que :
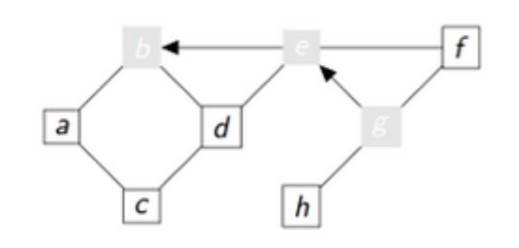
2nd tour
sommet = b
vu = [g,e,b]
aVoir : [h,f,d,a]
Au troisième tour de la boucle tant que :
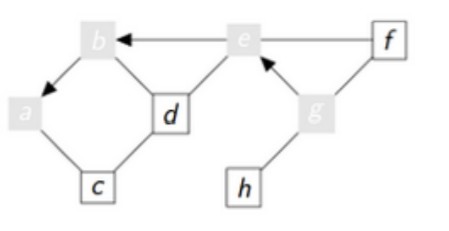
3ème tour
sommet = a
vu = [g,e,b,a]
aVoir : [h,f,d,c]
Au quatrième tour de la boucle tant que :
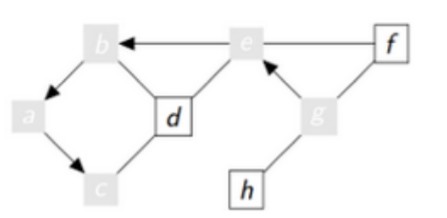
4ème tour
sommet = c
vu = [g,e,b,a,c]
aVoir : [h,f,d]
Au cinqième tour de la boucle tant que :
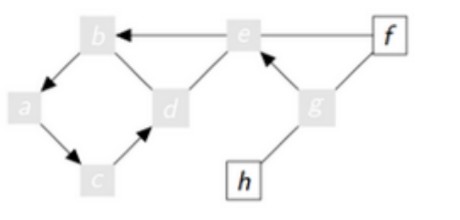
5ème tour
sommet = d
vu = [g,e,b,a,c,d]
aVoir : [h,f]
Au sixième tour de la boucle tant que :
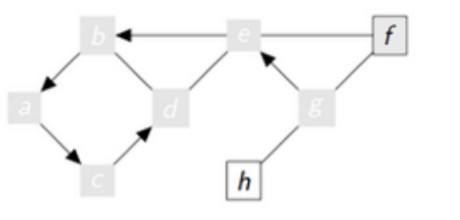
6ème tour
sommet = f
vu = [g,e,b,a,c,d,f]
aVoir : [h]
Au septième tour de la boucle tant que :
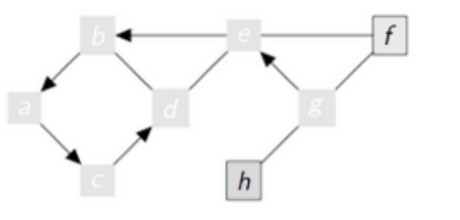
7ème tour
sommet = h
vu = [g,e,b,a,c,d,f,h]
aVoir : []
la boucle s'arrête
 | la liste aVoir est utilisée comme une PILE. On empile les voisins du sommet que l'on visite, puis on les dépile, c-a-d qu'on repart du dernier sommet empilé. C'est pour cette raison que l'on parcours l'arbre en profondeur, on commence par les voisin du dernier sommet. Si on utilisait aVoir comme une file, on parcourrais en largeur (ce que nous ferons plus loin). |
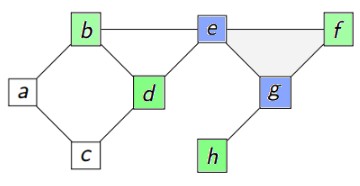
Voici une représentation schématique du parcours que nous venons de faire, si on représente le graphe avec G en haut, puis par couche selon la distance à G :
Implémentation non récursive de l'algorithme
Algorithme :
Placer le sommet de départ dans vus
Empiler les voisins de ce sommet dans aVoir
tant que aVoir n'est pas vide :
depiler le prochain sommet
l'ajouter dans vus
ajouter ses voisins non vus et non à voir dans aVoir
Implémentation récursive de l'algorithme DFS
Algorithme :
DFS(gr , sommet , vus) :
Placer le sommet de départ dans vus
pour chaque voisin de liste des voisins de ce sommet :
si le voisin n'est pas déjà vu :
DFS(gr,voisin,vus)
renvoyer la liste vus
Activité débranchée : Recherche en LARGEUR d'abord BFS
https://cscircles.cemc.uwaterloo.ca/wp-content/uploads/deroule-bfs.pdf
Pour parcourir le graphes en largeur d'abord :
Algorithme de parcours BFS
- on commence avec un nœud donné (point de départ)
- on ajoute ce sommet dans vus
- on enfile les voisins de ce sommet dans aVoir
- tant que la FILE aVoir n'est pas vide :
- -- on defile le prochain sommet et on l'ajoute dans la liste vus
- -- on enfile ses voisins dans aVoir
Donc, parcourir un graphe en largeur à partir d’un sommet, consiste à explorer le graphe en explorant systématiquement tous les voisins d'un sommet avant de descendre dans la profondeur du graphe.
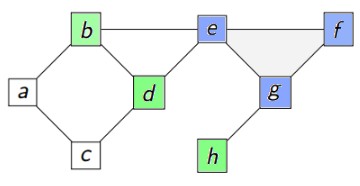
Voici les contenus des variables au premier tour de la boucle tant que :
Au début:
sommet = g
aVoir: [e,f,h]
1er tour de la boucle :
sommet=e
vus : [g,e]
aVoir = [f,h,d,b]
Au second tour de la boucle tant que :
2nd tour
sommet = f
vu = [g,e,f]
aVoir : [h,b,d]
Au troisième tour de la boucle tant que :
3ème tour
sommet = h
vu = [g,e,f,h]
aVoir : [b,d]
Au quatrième tour de la boucle tant que :
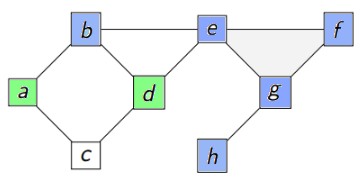
4ème tour
sommet = b
vu = [g,e,f,h,b]
aVoir : [d,a]
Au cinqième tour de la boucle tant que :
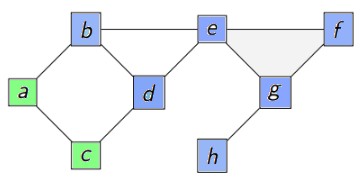
5ème tour
sommet = d
vu = [g,e,f,h,b,d]
aVoir : [a,c]
Au sixième tour de la boucle tant que :
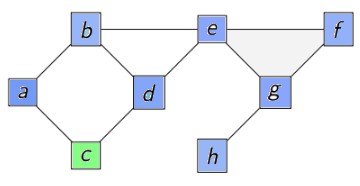
6ème tour
sommet = a
vu = [g,e,f,h,b,d,a]
aVoir : [c]
Au septième tour de la boucle tant que :
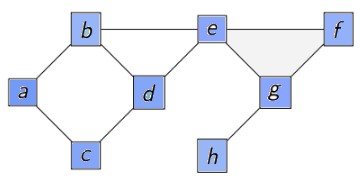
7ème tour
sommet = c
vu = [g,e,f,h,b,d,a,c]
aVoir : []
la boucle s'arrête
 | la liste aVoir est utilisée comme une FILE. On enfile les voisins du sommet que l'on visite, puis on les défile, c-a-d qu'on repart du premier sommet enfilé. C'est pour cette raison que l'on parcours l'arbre en largeur, on commence par les voisins des premier sommets visités. |
Voici une représentation schématique du parcours que nous venons de faire, si on représente le graphe avec G en haut, puis par couche selon la distance à G :
Implémentation (non récursive) de l'algorithme BFS
Algorithme :
Placer le sommet de départ dans vus
Enfiler les voisins de ce sommet dans aVoir
tant que aVoir n'est pas vide :
defiler le prochain sommet
l'ajouter dans vus
ajouter ses voisins non vus et non à voir dans aVoir



