T1.3 Révisions : Algorithmes à connaitre

Algorithmes de tris et dichotomie

Premier algo

fonction algo1(tableau) : 
        pour i allant de 0 à longueur(tableau)-2 :
                imin=i
                pour j allant de i+1 à len(tableau)-1 :
                        si tableau[j] < tableau[imin] :
                                imin=j
                        fin de si
                fin de pour
                if imin!=i:
                        tableau[i],tableau[imin]=tableau[imin],tableau[i]
                fin de si
        renvoyer tableau


Exercice à choix multiple 
L'algorithme ci-dessus correspond à ... 
Votre choix : 
Correct !

Exercice de code : ALGO 1

Coder le pseudo code donné au dessus.
Une liste lst sera générée pour vous pour la validation.
Dans la fonction, vous introduirez un comptage du nombre de comparaisons effectuées, qui sera affiché avant de sortir de la fonction (comme indiqué dans le code à compléter ci-dessus)

#cette ligne est requise pour la validation, ne pas vous en occuper
random.seed(codeInitRandom)
def algo1(lst:list) -> list :
    '''
    Effectue le tri d'une liste par --ALGO1--, renvoie la liste triée
    sans préserver la liste initiale (tri en place)
    '''
    # votre code ici

    print('nombre de comparaison : ',ncomp)
    return lst

print(algo1(lst))

Deuxième algo

fonction algo2(lst) : 

         pour i de 1 à len(lst) - 1
            # mémoriser lst[i] dans x
            x ← lst[i]                            

            # décaler vers la droite les éléments de lst[0]..lst[i-1] qui sont plus grands que x en partant de lst[i-1]
            j ← i                               
            tant que j > 0 et lst[j - 1] > x
                     lst[j] ← lst[j - 1]
                     j ← j - 1
            fin de tant que
            # placer x dans le "trou" laissé par le décalage
            lst[j] ← x 
       renvoyer lst


Exercice à choix multiple 
L'algorithme ci-dessus correspond à ... 
Votre choix : 
Correct !

Exercice de code : ALGO 2

#cette ligne est requise pour la validation, ne pas vous en occuper
random.seed(codeInitRandom)
def algo2(lst:list) -> list :
    '''
    Effectue le tri d'une liste par --ALGO2--, renvoie la liste triée
    sans préserver la liste initiale (tri en place)
   La fonction affiche dans la console le nombre de comparaisons effectuées
    '''
    # votre code ici

    print(' nombre de comparaison : ',ncomp)
    return lst

print(algo2(lst))

Comment interpréter les nombres de comparaison des algorithmes 2 et 3 ?

Pouvez vous donnez le nombre de comparaisons de l'algo 1 pour une liste de 200 valeurs ?

Pour l'algo2, que pourrait on dire ?

Et quelle est la complexité de l'algo 3 ?

Troisième algo

fonction algo3(x,lst) :


    imin=0
    imax=len(lst)-1   
    imilieu=(imin+imax)//2
    tant que imin <= imax :
        si lst[imilieu]>x             
             # on va chercher dans la partie de gauche :
             imax=imilieu-1
        sinon si lst[imilieu] < x :
             # on va chercher dans la partie de droite:
             imin=imilieu+1
        sinon :
             # on a trouvé x 
             renvoyer True
        fin de si
        imilieu=(imin+imax)//2
     fin de tant que
     renvoyer False


Exercice à choix multiple 
L'algorithme ci-dessus correspond à ... 
Votre choix : 
Correct !

S'il vous reste du temps...

Modulo 7

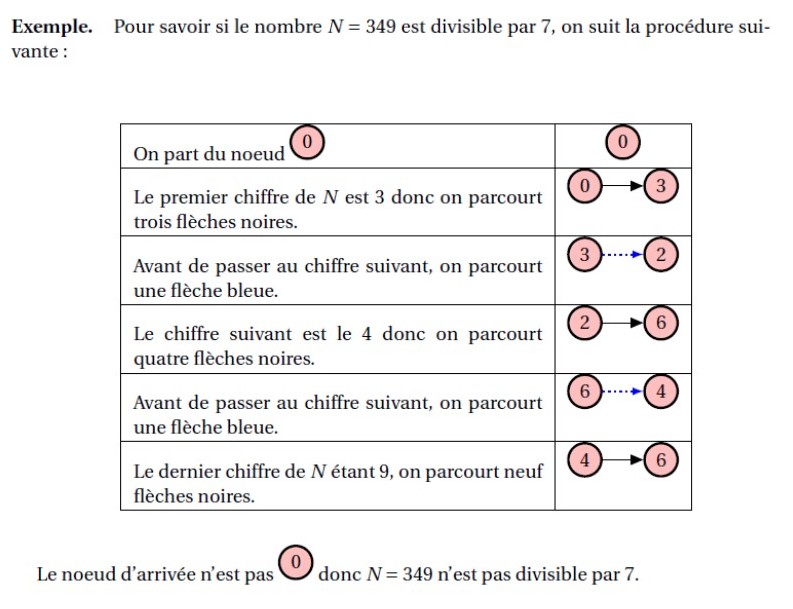
Voici un graphe (nous étudierons les graphes plus en détail bientôt) qui permet de calculer N%7 pour tout nombre entier N :

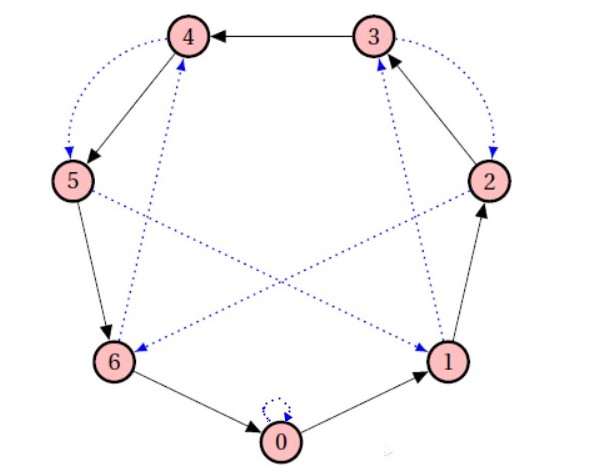
Ce graphe contient des flèches noires et des flèches bleues. Votre premier travail est de modéliser le graphe avec deux dictionnaires : BLACK et BLUE.

Dans chacun des dictionnaires, les clés sont les valeurs de départ des flèches (noires ou blueues) et les valeurs sont les valeurs d'arrivée.

Par exemple, dans le dictionnaire NOIR, la clé 0 à pour valeur 1.

Ensuite, vous devez implementer l'algorithme de détermination de N%7. Etudions un exemple :