T 3.4 Parcours récursifs d'itérables

Reprenons un exemple de Compteur en impératif: compter le nombre de valeurs paires d'une liste.

Exemple : Un exemple d'utilisation d'un Compteur. nbMult2 est le compteur.

def nbrePairs(lst: list ) -> int: """ :param lst: type list : une liste de nombres entiers :returns: type int : le nombre de valeurs paires dans la liste """ nbMult2 = 0 for element in lst: if element % 2 == 0: nbMult2 += 1 return nbMult2 print(nbrePairs([1, 2, 3, 4, 6]))

---

Comment faire la même chose en mode récursif

---

Notre compteur nbMult2 dans la fonction nbrePairs(lst) peut se concevoir de façon récursive comme :
nbMult2 = (1 si l[0] est pair, 0 sinon) + nbrePairs du reste de la liste
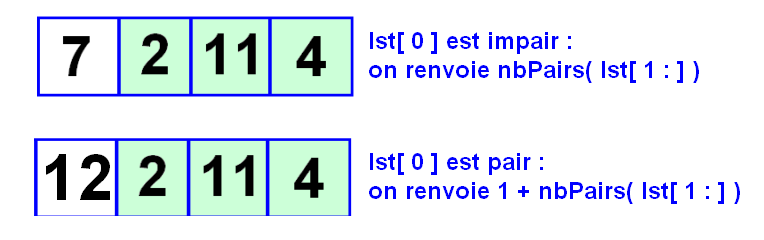
Si le 1er nombre est pair on renvoie 1 + nombre pair du reste
Si le 1er nombre est impair on renvoie 0 + nombre pair du reste

Par exemple : nb=nbPairs([1, 2, 3, 4, 6]) :

renvoyer 0 + nbPairs([2, 3, 4, 6])................................. # 0 car 1 est impair
renvoyer 0 + (1 + nbPairs(3, 4, 6]) )...............................# 1 car 2 est pair
renvoyer 0 + (1+ ( 0 + nbPairs([4, 6]) )........................# 0 car 3 est impair
renvoyer 0 + (1+ ( 0 + 1 nbPairs([6]) ) ) ) ................. # 1 car 4 est pair
renvoyer 0 + (1+ ( 0 + ( 1 + ( 1 + ( nbPairs([]) ) ) ) ).. # 1 car 6 est pair
renvoyer 0 + (1+ ( 0 + ( 1 + ( 1 + ( 0 ) ) ) ).. # fin, on appelle plus la fonction !

Et quand il n'y a aucun élément (liste vide) : nbPairs([]) = 0

• La longueur de la liste décroit, la liste finira par être vide
• le nombre d'élément pairs es bien égal à ce qu'on renvoie

Exemple : Un exemple de transposition du compteur en mode récursif

def nbrePairs(lst:list ) -> int: """ :param: lst de type list : une liste de nombres entiers :returns: de type int : le nombre de valeurs paires dans la liste """ if len(lst) == 0 : return 0 else : if lst[0] %2 == 0 : pair = 1 else : pair = 0 return pair + nbrePairs(lst[1:]) print(nbrePairs([1, 2, 3, 4, 6]))

La condition d'arrêt : si lst est vide, nb=0, s'écrit :

if len(lst) == 0:
    return 0

Exercices avec un compteur

Exercice de code : combien de fois ?

Ecrire une fonction récursive qui compte le nombre d'occurrence d'une lettre dans un texte.

Vous devez créer un compte et vous connecter avant de poser une question.

def compter(lettre: str , txt: str ) -> int: ''' renvoie le nombre d'occurrences de lettre dans txt >>> compter('e','ceci est un texte') 3 ''' # vous devez coder la fonction en mode récursif

Plus d'actions... Réinitialiser code Aide

Exercice de code : Longueur

compter le nombre d'éléments dans un iterable mutable (liste ou chaine).

Dans cette version utilisant le slicing, on envisage seulement les cas d'itérable str ou list

Vous devez créer un compte et vous connecter avant de poser une question.

def longueur( iterable ) -> int: ''' renvoie la longueur d'un iterable mutable. >>> longueur('ceci est un texte') 17 >>> longueur([1,2,3]) 3 L'argument doit être une liste ou une chaine ''' # vous devez coder la fonction en mode récursif

Plus d'actions... Réinitialiser code Aide

Dans les exemples que nous avons traité, nous avons utilisé le slicing avec des instructions comme :

somme(lst[1:])

Pour exécuter une telle instruction, l'interpréteur python va dupliquer la liste (sauf le premier élément). La complexité de cette opération est O(n). Si cette opération doit être réalisé à chaque appel et qu'on fait N appels, on se retrouve avec une complexité en O(n²) alors qu'on a un algorithme en O(n). C'est donc bien commode mais plutôt désastreux.

Nous allons voir comment éviter ces copies de lites, donc coder sans slicing.

Commençons par un exemple.

On veux écrire une fonction estTriee(lst) qui renvoie True si la liste est triée (croissante) et False sinon.

Une version impérative pourrait être :

Exemple

Détermine (en impératif) si une liste est triée ou non

def estTriee(lst: list) -> bool: """ :param: lst de type list : liste de nombres entiers :returns: de type booléen: True si la liste est triée croissante, False sinon. """ for i in range(len(lst) - 1): if lst[i] > lst[i+1]: return False return True print(estTriee([1, 2, 3, 4])) print(estTriee([1, 2, 3, 1]))

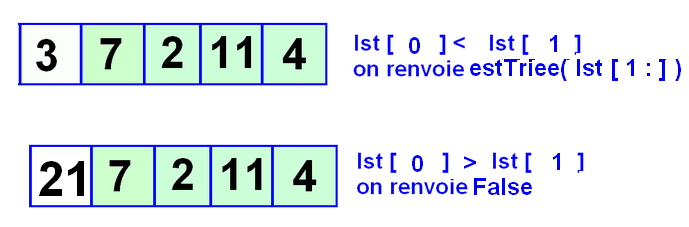
Ce problème est clairement récursif. On compare 2 éléments (on commence par les 2 permiers) et on vérifie l'ordre. Si l'ordre est mauvais on renvoie False, sinon au continue sur le reste de la liste.

Il n'y a pas à proprement parler de curseur dans cette fonction, mais la technique reste quand même assez similaire. Une variante serait de renvoyer la position du premier élément non ordonné, et on aurait vraiment un curseur. Mais nous allons rester sur la version plus simple donnée ci-dessus..

1ere version : en utilisant des slices, pour découper la partie de liste restant à traiter.

Exemple

Détermine (en récursif) si une liste est triée ou non

def estTriee(lst: list) -> bool: """ :param: lst est de type list : liste de nombres entiers :returns: de type bool. True si la liste est triée croissante, False sinon. """ if len(lst) == 1: return True if lst[0] < lst[1] : return estTriee(lst[1:]) else: return False print(estTriee([1, 2, 3, 4])) print(estTriee([1, 2, 3, 1]))

Ce code fonctionne et il est assez similaire à la version non récursive.

L'algorithme est clairement de complexité linéraire (n-1 comparaison)

Mais notre code n'est pas de complexité linéaire ! En effet, à chaque exécution de estTriee, on effectue une copie de lst.

Pour une longueur N, je dois rappeler estTriee avec une longueur n-1, et je dois copier n-1 élément dans une nouvelle liste. Le temps d'éxécution peut s'ecrire :

T(n) = T-1) + T(n-1) + n

Pour comprendre cette formule, prenons une analogie :

Je dois éplucher n pommes de terre. Le temps que je vais mettre est en principe égal au temps d'éplucher une pomme de terre + le temps d'éplucher les n-1 restantes.

T(n) = T(1) + T(n-1) nous donne une complexité linéaire

Mais imaginons que après chaque pomme de terre épluchée, je doive déplacer une à une toutes les pommes de terre restantes dans une autre pièce avant de poursuivre l'épluchage...

Le temps total sera alors :

T(n) = T(1) + T(déplacer une a une) + T(n-1)

Et comme je dois toutes les déplacer, le temps de déplacement sera proportionnel à n -1. Notons T' le temps pour déplacer une pomme de terre :

T(n) = T(1) + (n - 1) T' + T(n - 1)

Et donc

T(n) = T(1) + (n-1) T' + [  T(1) + (n-2) T' + T(n-2) ]
     = 2 . T(1) + [(n-1) + (n-2)] T' + T(n-2)
     = 2 . T(1) + [(n-1) + (n-2)] T' + [  T(1) + (n-3) T' + T(n-3) ]                      
     = 3 . T(1) + [(n-1) + (n-2) + (n-3)] T' + T(n-3)

Etc.... on arrivera à :

T(N) = N . T(1) + (1 + 2 + ... + n-1) T'

et on reconnait la somme

Cette formule de récurrence mène donc à une complexité en O(n²).

Retenir :

Si le cas général est en temps constant : T(N) = O(1) + T(N-1) -> complexité linéaire O(N)

Si le cas général est en temps proportionel à N: T(N) = O(N) + T(N-1) -> complexité quadratique O(N²)

Pour éviter le slicing, il va falloir utiliser les indices. En impératif, nous disposons de l'itérateur qui parcours aisément la liste. En récursif c'est plus délicat, et pour y parvenir nous allons devoir ajouter un attribut à notre fonction.

Au départ il vaudra 0, et nous allons lui attribuer cette valeur par défaut.

A chaque appel de estTriee( lst, n )

• on compare lst[n] à lst[n+1]
  • Si les deux valeur sont dans l'ordre on reprend en incrémentant n
  • sinon on renvoie False :

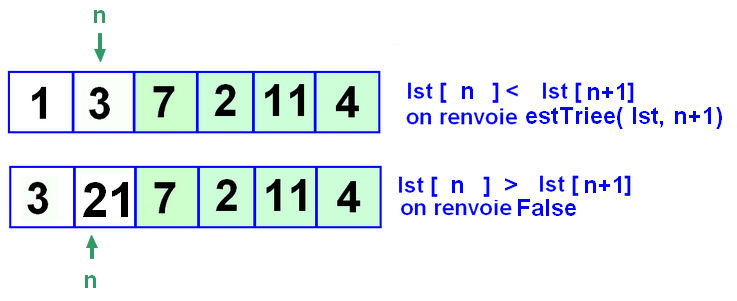
On s'arrêtera au dernier, qu'on aura pas besoin de comparer au suivant puisqu'il n'y a plus de suivant.

Le cas de base est donc : si n = len(lst) - 1 renvoyer True

Exemple

Détermine (en récursif et sans slice) si une liste est triée ou non

def estTriee(lst: list, n = 0) -> bool: """ :param lst: de type list : liste de nombres entiers :param n: de type int, qui est la valeur que nous devons comparer à la suivante. :returns: True si la liste est triée croissante, False sinon. """ if n == len(lst) - 1 : # dernier élément, la liste est donc triée return True if lst[n] < lst[n+1] : # les éléments sont dans l'ordre, on passe au suivant return estTriee(lst, n+1) else : return False # on a trouvé un élément non trié print(estTriee([1, 2, 3, 4])) print(estTriee([1, 2, 3, 1]))

Ici le cas général et constitué d'un simple test de comparaison, une affectation, et un appel, c'est bien en temps constant : T(N) = T(1) + T(N-1)

La complexité du code est donc linéaire O(N).

Retenir :

Pour connaitre l'indice de l'élément en cours de traitement :

° Définir un paramètre avec valeur par défaut égale à 0

° A chaque appel, incrémenter ce paramètre

Exercices

Reprendre les 2 codes des accumulateurs et les réécrire en n'utilisant pas de slice.

Somme des éléments d'une liste

Exercice de code : Somme des éléments d'une liste (récursivement sans slice)

Le code fourni utilise des slice. Vous devez le modifier pour parcourir la liste sans utiliser de slicing.

Vous devez créer un compte et vous connecter avant de poser une question.

def somme(lst: list) -> int: """ :param lst: une liste d'entiers :returns: de type int : la somme des éléments de la liste """ if lst == [] : return 0 else : return lst[0] + somme(lst[1:])

Plus d'actions... Réinitialiser code Aide

Nombre d'élément pairs dans une liste

Exercice de code : Compter le nombre d'éléments pairs en récursif et sans slice

Le code fourni utilise des slices. Vous devez le modifier pour parcourir la liste sans utiliser de slicing.

Vous devez créer un compte et vous connecter avant de poser une question.

def nbrePairs( lst:list ) -> int: """ :param lst: de type list : une liste de nombres entiers :returns: de type int : le nombre de valeurs paires dans la liste """ if len(lst) == 0 : return 0 else : if lst[0] %2 == 0 : pair = 1 else : pair = 0 return pair + nbrePairs(lst[1:]) print(nbrePairs([1, 2, 3, 4, 6]))

Plus d'actions... Réinitialiser code Aide

Si vous n'aimez pas les paramètres par défaut....

Il existe une autre façon de procéder. L'idée est la même : ajouter un paramètre. Mais au lieu d'en ajouter un avec une valeur par défaut, on crée purement et simplement une autre fonction :

Exemple

Détermine (en récursif et sans slice) si une liste est triée ou non

def estTriee(lst: list ) -> bool: """ :param: lst de type list : liste de nombres entiers :returns: True si la liste est triée croissante, False sinon. """ return estTrieeRec(lst, 0) def estTrieeRec(lst, n): """ :param: lst de type list : liste de nombres entiers :param n: indice de l'élément qu'on doit comparer lors de cet appel :returns: True si la liste est triée croissante, False sinon. """ if len(lst) - 1 == n: # on est au dernier élément, la liste est donc triée return True if lst[n] < lst[n+1]: # les éléments sont dans l'ordre, on passe au suivant return estTrieeRec(lst, n+1) else : return False print(estTriee([1, 2, 3, 4])) print(estTriee([1, 2, 3, 1]))

RETENIR

Le problème des traitements récursifs d'itérables est un peu différent, on ne dispose pas d'un itérateur comme dans la boucle for, et pourtant on itère...

1er solution : on fait du slicing
exemple :

def somme_lst(lst) :   
     if len(lst) == 0 : 
         return 0    
     return lst[0]  + somme_lst(lst[1:])

C'est plutot simple, et élégant, mais cela à un coût ( en 0(n) ) et c'est donc peu recommandé d'autant plus si on prend aussi en compte la complexité en espace.

2eme solution : un paramètre par défaut (ou plusieurs)

exemple :

def somme_lst(lst, n = 0) :
    if n == len(lst) : 
        return 0
    return lst[n]  + somme_lst(lst, n+1)

3eme solution : une fonction intermédiaire ou une fonction locale

exemple 

def somme_lst(lst ) :
    return somme_lst_rec(lst, 0)

def somme_lst_rec(lst, n) :
    if n == len(lst) : 
        return 0
    return lst[n]  + somme_lst_rec(lst, n+1)

variante avec fonction locale :
def somme_lst(lst) :
    def somme_lst_rec(lst, n):
        if n == len(lst): 
            return 0 
        return lst[n]  + somme_lst_rec(lst, n+1)
    return somme_lst_rec(lst, 0)

---

Les curseurs sont utilisés lorsqu'on doit scanner un itérables pour repérer un éléments selon un critère. Par exemple le plus grand, ou la dernière (ou première) occurrence d'une valeur, ou le premier (ou dernier) multiple d'un nombre, ou une clef d'un dictionnaire ayant une valeur donnée etc...

Les codes sont présentés pour une recherche du max mais peuvent aisément être adaptés pour la recherche du min.

Recherche du max : on déplace le curseur en notant la valeur la plus grande

Avant de débuter notons que rechercher le max dans une liste vide n'a pas de sens. Nous ne considérerons que des listes non vides

La version itérative :

• on initialise vmax à lst[0]
• Du 1er au dernier élément :
  • si l'élément est plus grand on actualise vmax

Exemple : Un exemple d'utilisation d'un Curseur. vmax est le curseur

def getMax(lst: list) -> int: """ :param: lst est une liste de nombres entiers :returns: de type int : le plus grand nombre. Si plusieurs nombre sont égaux dans la liste, la fonction renvoie l'un de ces éléments. La liste en entrée doit être non vide """ assert lst != [],"getMax : la liste doit être non vide" vmax = lst[0] for i in range(1, len(lst)): if lst[i] > vmax: vmax = lst[i] return vmax print(getMax([1, 2, 3, 4, 2]))

Les curseurs et la récursion

---

Envisageons un exemple : la recherche de la plus grande valeur dans une liste de nombres : lst = [1, 3, 7, 2, 11, 4] le max est 11.

Si on pense en récursif ici, cela donne :

Exemple

def getMax(lst: list) -> int: '''' recherche récursive de la valeur max dans une liste d ' entiers ''' if len(lst) == 1: return lst[0] else : vmaxReste = getMax(lst[1:]) if lst[0] >vmaxReste: vmax = lst[0] else : vmax = vmaxReste return vmax print(getMax([1, 2, 5, 2, 1]))

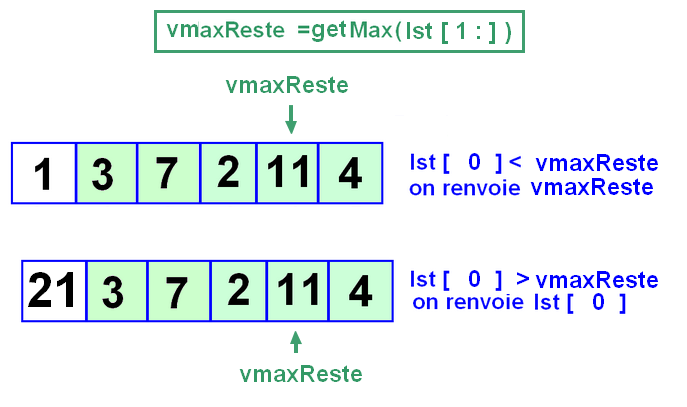
Dans ce code, nous avons écrit : vmaxReste = getMax(lst[1:]) if lst[0] >vmaxReste: vmax = lst[0] else : vmax = vmaxReste return vmax Nous avons donc d'abord appelé getMax avant de renvoyer la bonne valeur. Pourquoi ? On aurait put écrire : : if lst[0] > getMax(lst[1:]) return lst[0] else : return getMax(lst[1:]) Mais quel problème cela pose-t-il ? Pour vous aider, visualiser le code qui a été recopié ci-dessous, puis comparer en visualisant également le code précédant. N'oubliez pas de choisir la langue anglaise.

Exemple

def getMax(lst: list) -> int: '''' recherche récursive de la valeur max dans une liste d ' entiers ''' if len(lst) == 1: return lst[0] else : # vmaxReste = getMax(lst[1:]) if lst[0] > getMax(lst[1:]): return lst[0] else: return getMax(lst[1:]) print(getMax([12, 2, 5, 2, 1, 10]))

Et pour le faire sans slice ?

On introduit un second paramètre, dont la valeur par défaut est 0, qui est l'indice de l'élément en cours de traitement.

Par exemple, si n = 1 :

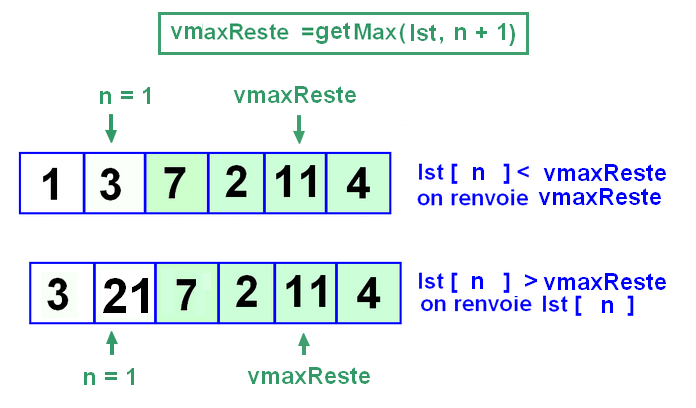
Et le cas de base sera n = len(lst) - 1 : un seul élément donc c'est lui le max, on renvoie lst[n]

Exercice de code

Vous devez créer un compte et vous connecter avant de poser une question.

def getMax(lst: list) -> int: ''' recherche récursive de la valeur max dans une liste d ' entiers ''' if len(lst) == 1: return lst[0] else : vmaxReste = getMax(lst[1:]) if lst[0] > vmaxReste : return lst[0] else: return vmaxReste print(getMax([12, 2, 5, 2, 1, 11]))

Plus d'actions... Réinitialiser code Aide

Cas de la recherche de l'indice du max : on déplace le curseur en notant l'indice

Dans le cas ou l'on recherche l'indice du max de façon récursive, nous allons devoir bien comprendre un point plus délicat : l'indice d'une valeur dans lst[1:] n'est pas le même que l'indice de la même valeur dans lst.

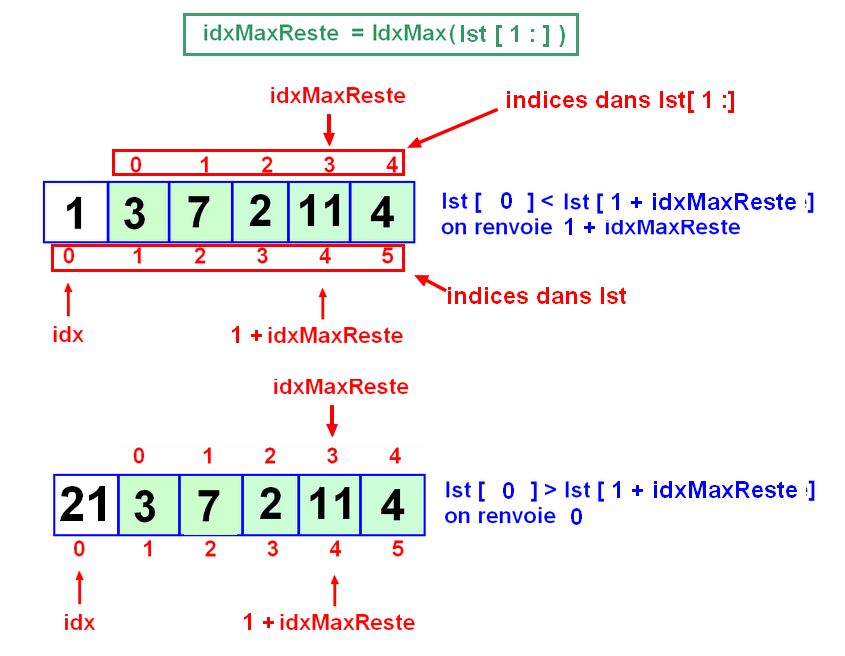
Ce qu'il faut bien comprend c'est le 1 + indice du max du reste.

La fonction s'écrira donc :

Exemple : Un exemple d'utilisation d'un Curseur en récursif

def idxMax(lst): if len(lst) == 1: return 0 else: idxMaxReste = 1 + idxMax(lst[1:]) if lst[0]>lst[idxMaxReste]: idx = 0 else : idx = idxMaxReste return idx print(idxMax([1, 2, 3, 4, 2]))

la ligne clé est :

        idxMaxReste = 1 + idxMax(l[1:])

L'utilisation du curseur est donc un peu plus compliquée à bien comprendre. En fait, idx est l'indice du max dans la liste, mais dans la fonction appelante, qui contient un élément de plus en tête, l'indice est idx + 1. Une fois bien compris ceci, l'utilisation de curseur ne devrait plus vous poser de difficulté.
La condition d'arrêt si len(l) == 1 : return 0 est intuitive

Une autre approche : un argument supplémentaire par défaut

Dans ces situations, comme pour le cas de la fonction estTriee, une autre approche peut se révéler plus intuitive, mais elle nécessite l'utilisation d'un paramètre supplémentaire qui doit avoir une valeur par défaut.

Rappelons le principe d'un paramètre avec valeur par défaut :

def f(x, n = 0):
    pass
# appel sans le second paramètre :
f(2) # x vaudra 2 et n vaudra 0
f(2) est identique à f(2,0) ou f(2, n=0 )

# appel avec 2 paramètres :
f(2, 3) ou f(2, n=3) # x vaudra 2 et n vaudra 3

La fonction sera définie ainsi :

def idxMax(lst: list, idx = 0)

Exemple : chercher l'indice du max dans [ 1 , 3 , 4 , 2 ]

1er appel : getIdxMax( [1 , 3 , 4 , 2 ] )

idx vaut 0 : on cherche dans toute la liste

On renvoie le plus grand entre lst[0] et getIdxMax(lst, 1)

2ème appel idx vaut 1, On renvoie l'indice associé à la plusgrande valeur (on compare lst[1] et lst[ getIdxMax(lst, 2) ]

Voir ci-dessous, par exemple un appel avec idx = 2 :

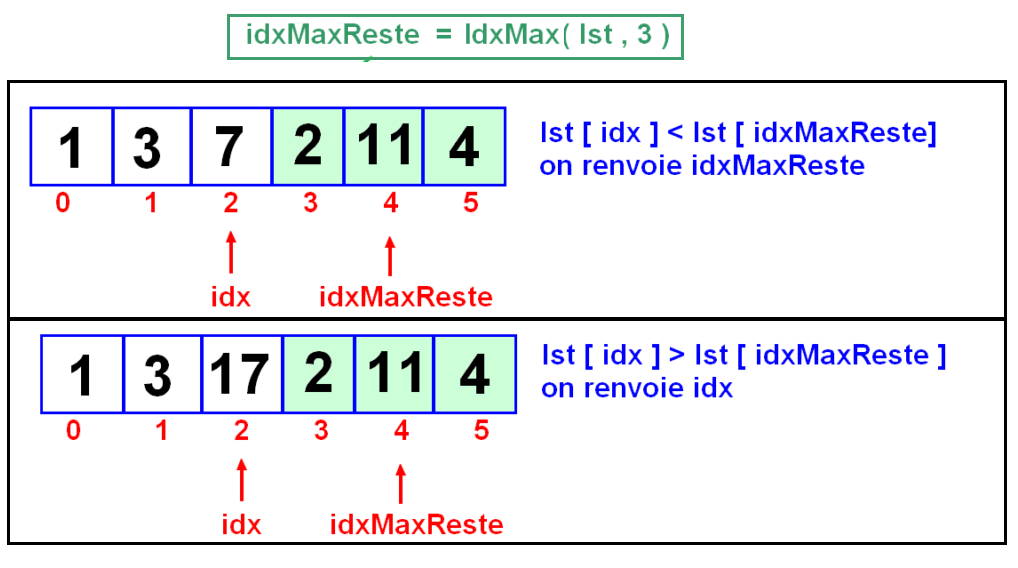
etc... et on arrête quand idx et l'indice du dernier élément, c'est-à-dire len(lst) - 1. Dans ce cas l'indice du max est idx puisqu'on ne cherche que parmi le dernier élément.

L'algorithme peut être décrit ainsi :

cas général :
idxMaxReste = indice_du_max(lst, idx + 1) (indice du plus grand dans le reste de la liste)
on renvoie idx si lst[idx] > lst[idxMaxReste] sinon on renvoie idxMaxReste
cas de base :
si idx est l'indice du dernier, il n'y a pas de reste de la liste. On renvoie idx

On se rend compte que les curseur récursifs sans slice sont bien plus simple qu'avec slice, et même plus naturel que la version itérative.

A vous :

Exemple : Un exemple d'utilisation d'un Curseur sans slice.

def idxMax(lst: list, idx = 0): if len(lst) - 1 == idx: return idx else: idxMaxReste = idxMax(lst, idx+1) if lst[idxMaxReste] > lst[idx]: idx = idxMaxReste return idx print(idxMax([1, 2, 3, 4, 2])) print(idxMax([1, 2, 3, 4, 2, 7])) print(idxMax([7, 1, 2, 3, 4, 2, 5]))

Les deux versions de ce code ne sont pas du tout équivalentes. La première utilise des slices lors de l'appel avec lst[1:]. Cela induit des coûts importants de temps de calculs et de coût en mémoire, car python va dupliquer la liste. La seconde version utilise l'indice et ne requiert aucune copie de liste. Elle sera bien plus efficace en temps et en espace.

On vous demande de coder une version récursive de la fonction appartient donnée ci-dessous :

Exemple : Recherche de l'appartenance

def appartient(x: int, lst: list) -> bool: """ :param x: de type int :param list : une liste d'entiers :returns: de type bool : True si x est dans la liste, False sinon """ for element in lst: if element == x: return True return False assert appartient(5, [5, 2, 4, 3]) == True assert appartient(3, [5, 2, 4, 3]) == True assert appartient(2, [5, 2, 4, 3]) == True assert appartient(0, [5, 2, 4, 3]) == False assert appartient(8, [5, 2, 4, 3]) == False

1ère version : avec slicing:

Exercice de code : Appartenance d'un élément à une liste (récursivement)

Vous devez créer un compte et vous connecter avant de poser une question.

def appartient(x:int, lst:list) -> bool: """ :param x: de type int :param list : une liste d'entiers :returns: de type bool : True si x est dans la liste, False sinon """ # cas de base : si on a 1 seul élément if ...: return ... else : # cas général : a vous de trouver ! return ...

Plus d'actions... Réinitialiser code Aide

2ème version : Sans slicing (paramètre par défaut ou fonction intermédiaire) :

Exercice de code : Appartenance d'un élément à une liste (récursivement)

Vous devez créer un compte et vous connecter avant de poser une question.

def appartient(x: int, lst: list, idx = 0) -> bool: """ :param x: de type int :param list : une liste d'entiers :returns: de type bool: True si x est dans la liste, False sinon """ # cas de base: si on a plus d'élément if ... : return ... else : # cas général : # renvoyer True si lst[idx] est l'élément cherché ou si x appartient au reste de la liste return ... or ...

Plus d'actions... Réinitialiser code Aide