Exemples
Nous désirons créer un programme qui produise cette figure :
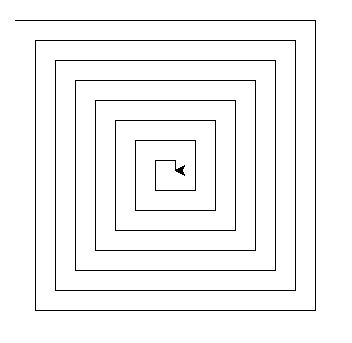
Pour cela nous allons utiliser le module turtle de façon très basique.
 | Vous devez commencer par vous connecter à votre compte replit pour faire les activités de dessin Turtle. Ensuite, vous cliquez sur le lien désiré, puis une fois le lien ouvert, en haut à droite, sur open in replit. Si ce n'est pas actif, bien penser à fermer toutes les boites de dialogues qui ont été ouvertes. Une fois la fenêtre de replit ouverte, il faudra cliquer en haut à droite sur Fork |

Decouvrir Turtle : Si tu ne connais pas Turtle, ouvre le lien Découverte de Turtle en haut de la page pour apprendre les instructions de base dont nous aurons besoin.
Passons au dessin proprement dit
La récursivité en action : Utilise le lien Dessin récursif en haut de la page
Par exemple, nous voulons écrire un programme qui produit le dessin ci-dessous avec turtle. Cela semble assez difficile.
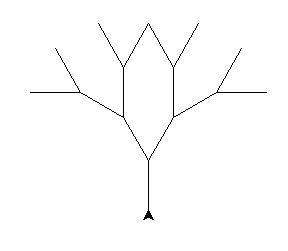
Le code utilisant une fonction récursive est finalement assez simple à imaginer .
Utiliser le lien Dessin récursif 2 en haut de la page pour voir sa structure
Nous voulons créer une fonction qui calcule an sans utiliser la fonction puissance.
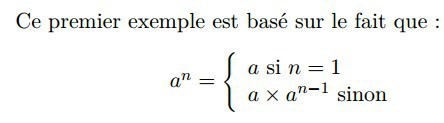
Regardons ce qu'il se passe si on appelle puiss(3,4)
De façon triviale puiss(3,1) renvoie 3.
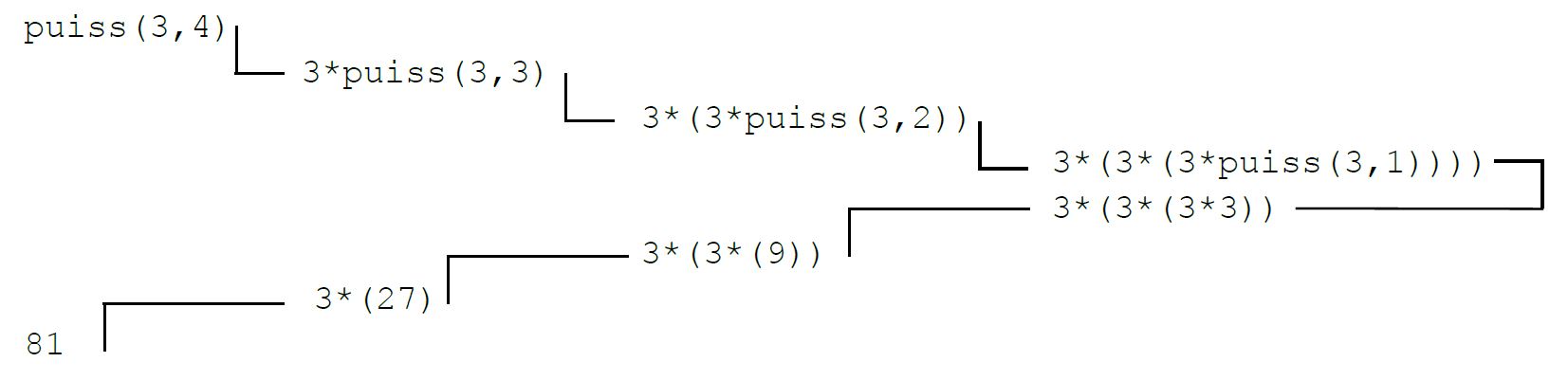
Fonctions récursives
La récursivité est une méthode de résolution de problèmes qui consiste à décomposer le problème en sous-problèmes identiques de plus en plus simples jusqu'à obtenir un problème suffisamment simple qui puisse être résolu de manière évidente (triviale).
On peut appeler ce problème très simple : cas de base, ou cas trivial.
Dans l'exemple précédant le cas de base est : puiss(a,1) qui renvoie a.
Le plus souvent nous utilisons une fonction récursive, lorsque cela est beaucoup plus simple à programmer qu'un programme itératif (décomposition en sous-problèmes identiques de plus en plus simples).
Python s'arrête au bout d'un certain nombre d'appels récursifs, et affiche le message d'erreur. Il manquait dans cette fonction le cas de base :
if n == 1 :
return a
Python limite explicitement le nombre d’appels récursifs dans une fonction. Ainsi, après 1000 appels récursifs, l’interpréteur Python va lever l’exception RecursionError et afficher le message d’erreur suivant : RecursionError: maximum recursion depth exceeded.
Cette limite, fixée à 1000 appels récursifs, est une valeur par défaut qu’il est possible de modifier en utilisant la fonction setrecursionlimit disponible dans le module sys. Par exemple, pour passer cette limite à 2000 appels maximum, on exécutera le code Python suivant :
import sys
sys.setrecursionlimit(2000) Source : spécialité Numérique et sciences informatiques, 24 leçons avec exercices corrigés classe de terminale - ellipses
Il peut y avoir un autre problème si les appels récursifs successifs éloignent du cas de base au lieu d'en rapprocher.
Reprenons la fonction puiss() écrite plus haut de façon récursive.
Ici puiss(4, -1) appelle puiss(4, -2), qui appelle puis(4, -3) etc...
On n'atteindra jamais le cas de base qui aurait été puiss(4, 1), et le processus est infini.
- Trouver le cas général : trouver l'élément de récursivité qui permet de décomposer le problème en cas plus simple.
- Trouver le cas de base : trouver la condition d'arrêt, et la solution du problème dans ce cas particulier. La condition d'arrêt sera bien atteinte après un nombre fini d'appels. Chaque appel récursif tend à se rapprocher du cas de base.
- Réunir ces deux cas dans le programme : Le programme ne contient aucune boucle (
forouwhile) dans la partie qui résout le problème. Le programme contient un général une structureif/elseintroduisant le cas de base
Alice a réalisé le code suivant pour savoir si un entier se trouve dans un tableau (typ list python). C'est une recherche par dichotomie utilisant une fonction récursive.
Malheureusement, ce code ne fonctionne pas. Elle a donc demandé de l'aide à son ami Bob pour rectifier ce script. Vous êtes Bob, à vous de jouer !
Vous devez vous aider du bouton "visualiser" pour comprendre le déroulement du code proposé par Alice.
Compléter la fonction suivante, écrite de façon récursive, pour qu'elle retourne True si un entier est pair, et False sinon.
Vous ne pouvez pas utiliser le modulo %, ni la division /, ni la division entière //
Aide 1 Aide 2



