11C: Geometri

11. derste bulunan A, B, C bölümlerini istediğiniz sırayla tamamlayabilirsiniz.

Bu alıştırmada geometri hesaplamaları yapmak amacıyla dört fonksiyon oluşturacağız:

  • Bir dik üçgenin hipotenüs uzunluğunu hesaplayacak bir fonksiyon,
  • Bir dik üçgenin çevresini hesaplayacak bir fonksiyon,
  • 2D'de iki nokta arasındaki mesafeyi hesaplayacak bir fonksiyon,
  • Ve herhangi bir üçgenin çevresini hesaplayacak bir fonksiyon.

Hipotenüs

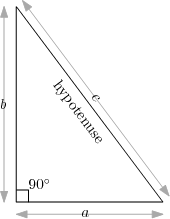Şekilde sağa doğru bakan bir dik üçgen var. Dik üçgen bilindiği gibi açılarından biri 90 derece (dik açı) olan üçgendir ve üç kenarı vardır. Dik açının karşısındaki kenara hipotenüs adı verilir.

Diyagramda gösterildiği gibi, dik açıya bitişik kenarlara a ve b, hipotenüse de c diyelim. Ünlü Pisagor teoremi bize şunu söyler:

\displaystyle{a^2+b^2=c^2}

Birinci problemde ödevimiz bu teoremi, a ve b değerlerini kullanarak hipotenüsü hesaplayan bir fonksiyona çevirmek.

Programavimo pratimas: Hipotenüs
Diğer kenarları a ve b olan üçgenin, c hipotenüsünün uzunluğunu hesaplamak üzere hypotenuse(a, b) fonksiyonunu tanımlayın. İpucu
Žemiau įveskite testavimo veiksmus, pvz., print(myfunction("testiniai duomenys")).

Çevre

Bir üçgenin çevresi üç kenarın uzunluklarının toplamıdır. Yukarıdaki diyagrama göre çevre a+b+c olacak. Progamınızda hipotenüs doğru olarak hesaplanmış varsayalım (ilk kutudaki çözümü ikinci kutuya kopyalamanıza gerek yok).

Programavimo pratimas: Dik Üçgen
 hipotenüs(a, b) fonksiyonunu kullanarak, dik kenarları a ve b olan üçgenin çevresini hesaplayacak bir dikÜçgenÇevresi(a, b) fonksiyonu tanımlayın.
Žemiau įveskite testavimo veiksmus, pvz., print(myfunction("testiniai duomenys")).

2 Nokta Arasındaki Uzaklık

İki boyutlu düzelmde iki nokta arasındaki doğrular (Kartezyen koordinat sistemi) x ve y koordinatlarında belirlenir. İnputları koordinat düzleminden iki nokta olacak bir fonksiyon yazalım, output olarak da bu iki nokta arasındaki mesafeyi versin. Bu konuda bize hipotenüs fonksiyonu yardım edecek.

Daha detaylı olarak, ilk nokta (x1, y1), ikinci nokta da (x2, y2) koordiantlarında olsun, x1 ve y1 gerçek sayılar olacak. Burada temel fikir aşağıdaki şemada gösterilen dik üçgeni çizmek: (x1, y1) ve (x2, y2) noktaları arasındaki doğru hipotenüs olacak, bu yüzden uzunluğu iki nokta arasındaki mesafeye eşittir.

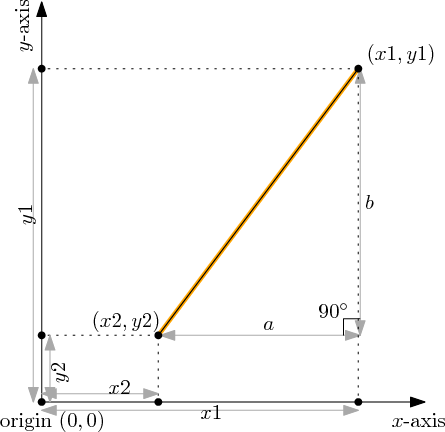
Hipotenüsü hesaplamak için üçgenin diğer iki kenarının uzunluklarını hesaplamamız lazım. Bunu koordinatların tanımını kullanarak yapabilirsiniz (şemaya bakabilirsiniz): yatay doğru a = x1-x2 ve dikey doğru b = y1-y2.

Programavimo pratimas: 2 Boyutlu Uzaklık
 hipotenüs(a, b) önceden tanımlanmış kabul ediyoruz. Bunu kullanarak tanımlayacağınız uzaklık2D(x1, y1, x2, y2) fonksiyonu (x1, y1) noktası ile (x2, y2) noktası arasındaki mesafeyi hesaplasın.
Žemiau įveskite testavimo veiksmus, pvz., print(myfunction("testiniai duomenys")).

Herhangi Bir Üçgenin Çevresi

Bu dersin son alıştırmasına geldik. Üçgenin çevresi üç kenarın uzunluklarının toplamı ve üçgenin bir kenarı da üçgenin iki köşe noktası arasında uzunluk demektir.

Programavimo pratimas: Çevreyi sabitle
Diyelim uzaklık2D(x1, y1, x2, y2) şu an için belirlenmiş olsun. Bunu alarak  üçgenÇevresi(xA, yA, xB, yB, xC, yC) fonskiyonunu tanımlayalım;  (xA, yA), (xB, yB) ve (xC, yC) noktalarından kenar uzunlukları ile üçgenin çevresini hesaplasın.
Žemiau įveskite testavimo veiksmus, pvz., print(myfunction("testiniai duomenys")).

Artık bir sonraki derse geçebiliriz!